题目内容
1. 如图所示长L=0.5m的轻杆,其一端固定于O点,另一端连有质量m=3kg的小球,它绕O点在竖直平面内做圆周运动.当小球运动到最高点时,取g=10m/s2.
如图所示长L=0.5m的轻杆,其一端固定于O点,另一端连有质量m=3kg的小球,它绕O点在竖直平面内做圆周运动.当小球运动到最高点时,取g=10m/s2.(1)轻杆对小球无作用力,小球的速度为多大;
(2)v=2m/s,杆受到的力的大小和方向;
(2)v=3m/s,杆受到的力的大小和方向.
分析 小球通过最高点时,由重力和杆对小球的作用力的合力提供向心力,以小球为研究对象,根据牛顿第二定律求解.
解答 解:(1)最高点,当杆对小球的作用力恰好为零,重力等于向心力,故:mg=m$\frac{{{v}_{0}}^{2}}{L}$,解得:${v}_{0}=\sqrt{gL}=\sqrt{0.5×10}=\sqrt{5}m/s$,
(2)v=2m/s<v0,则杆子对小球的作用力向上,根据牛顿第二定律得:
mg-T=m$\frac{{v}^{2}}{L}$
解得:T=6N
(3)v=3m/s>v0,则杆子提供拉力,方向向下,根据根据牛顿第二定律得:
mg+T′=m$\frac{{v}^{2}}{L}$
解得:T′=24N
答:(1)轻杆对小球无作用力,小球的速度为$\sqrt{5}m/s$;
(2)v=2m/s,杆受到的力的大小为6N,方向向上;
(2)v=3m/s,杆受到的力的大小为24N,方向向下.
点评 解决本题的关键知道“杆模型”中拉力与支持力的临界速度,分析物体受力,确定向心力的来源,再运用牛顿第二定律求解.

练习册系列答案
相关题目
12. 质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ,初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.设碰撞都是弹性的,则整个过程中,系统损失的动能为( )
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ,初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.设碰撞都是弹性的,则整个过程中,系统损失的动能为( )
 质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ,初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.设碰撞都是弹性的,则整个过程中,系统损失的动能为( )
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ,初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,并与箱子保持相对静止.设碰撞都是弹性的,则整个过程中,系统损失的动能为( )| A. | $\frac{1}{2}$mv2 | B. | μmgL | C. | $\frac{1}{2}$NμmgL | D. | $\frac{mM{v}^{2}}{2(m+M)}$ |
9.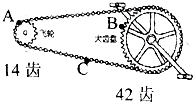 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点.现在提起自行车后轮,转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )| A. | A、B、C三点角速度大小相等 | |
| B. | A、B两点的线速度大小相等 | |
| C. | A、B两点的向心加速度之比为3:1 | |
| D. | 由图中信息,B、C两点的线速度之比为1:3 |
16.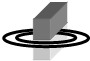 如图所示,两个同平面、同圆心放置的金属圆环a和b(a环面积大于b环),条形磁铁放在其中,通过两环的磁通量φa、φb相比较( )
如图所示,两个同平面、同圆心放置的金属圆环a和b(a环面积大于b环),条形磁铁放在其中,通过两环的磁通量φa、φb相比较( )
 如图所示,两个同平面、同圆心放置的金属圆环a和b(a环面积大于b环),条形磁铁放在其中,通过两环的磁通量φa、φb相比较( )
如图所示,两个同平面、同圆心放置的金属圆环a和b(a环面积大于b环),条形磁铁放在其中,通过两环的磁通量φa、φb相比较( )| A. | ?φa>φb | B. | φa<φb | C. | φa=φb | D. | 无法确定 |
6.下列说法正确的是( )
| A. | 日心说的代表人物是哥白尼 | |
| B. | 太阳是静止不动的,地球和其他行星绕太阳转动 | |
| C. | 地球是绕太阳运动的一颗行星 | |
| D. | 日心说和地心说都是错误的 |
13.用m表示地球同步通信卫星的质量、h表示卫星离地面的高度、M表示地球的质量、R0表示地球的半径、g0表示地球表面处的重力加速度、T0表示地球自转的周期、ω0表示地球自转的角速度,则地球同步通信卫星的环绕速度v不可能是( )
| A. | ω0R0 | B. | $\sqrt{\frac{GM}{{R}_{0}+h}}$ | C. | $\root{3}{Gm{ω}_{0}}$ | D. | $\root{3}{\frac{2πGM}{{T}_{0}}}$ |
10.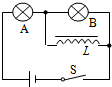 如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
 如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )| A. | 电键S断开时,A立即熄灭,而B会亮一下后才熄灭 | |
| B. | 电键S断开时,B立即熄灭,而A会亮一下后才熄灭 | |
| C. | 电键S闭合时,A、B同时亮,然后A熄灭 | |
| D. | 电键S闭合时,A、B同时亮,然后B逐渐变暗,直到不亮,A更亮 |
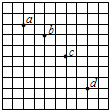 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: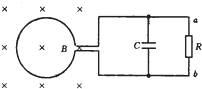 面积S=0.2m2、n=200匝的圆形线圈,处在如图所示的磁场内,磁感应强度随时间t变化的规律是B=0.02t,R=3Ω,C=30μF,线圈电阻r=1Ω,求:
面积S=0.2m2、n=200匝的圆形线圈,处在如图所示的磁场内,磁感应强度随时间t变化的规律是B=0.02t,R=3Ω,C=30μF,线圈电阻r=1Ω,求: