题目内容
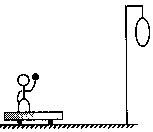
 如图所示,小朋友在玩一种运动中投掷的游戏,目的是在运动中将手中的球投进离地面高H=3m的吊环.他在车上和车一起以v车=2m/s的速度向吊环运动,小朋友抛球时手离地面h=1.2m,当他在离吊环的水平距离为s=2m时将球相对于自己竖直上抛,球刚好进入吊环,他将球竖直向上抛出的速度v0是
如图所示,小朋友在玩一种运动中投掷的游戏,目的是在运动中将手中的球投进离地面高H=3m的吊环.他在车上和车一起以v车=2m/s的速度向吊环运动,小朋友抛球时手离地面h=1.2m,当他在离吊环的水平距离为s=2m时将球相对于自己竖直上抛,球刚好进入吊环,他将球竖直向上抛出的速度v0是分析:将球相对于自己竖直上抛,实际上是球参与了两个运动,一是水平方向上的匀速直线运动,一是竖直方向上的竖直上抛运动,通过水平方向上求出运动时间,再结合竖直上抛运动的公式可求出上抛运动的速度.
解答:解:球的水平速度是v=2m/s,人到环的水平距离为s=2m,所以球必须在t=
=1s内到达吊环,则1s内球在竖直方向上的位移为x=1.8m,设初速度为v0,则根据竖直上抛运动的位移公式x=v0t-
at2有:
3-1.2=v0×1-
×10×12
解得:v0=6.8 m/s.
故答案为:6.8m/s.
| s |
| v |
| 1 |
| 2 |
3-1.2=v0×1-
| 1 |
| 2 |
解得:v0=6.8 m/s.
故答案为:6.8m/s.
点评:该题利用这种情境考查运动的合成与分解比较新颖,解题的关键就是知道合运动与分运动的等时性,小球的实际运动(相对于地面)是斜上抛运动,斜上抛运动可分解成水平方向的匀速直线运动和竖直方向上的竖直上抛运动.

练习册系列答案
相关题目
 如图所示,小朋友在玩一种运动中投掷的游戏,目的是在运动中将手中的球投进离地面高3m的吊环,他在车上和车一起以2m/s的速度向吊环运动,小朋友抛球时手离地面1.2m,当他在离吊环的水平距离为2m时将球相对于自己竖直上抛,球刚好进入吊环,他将球竖直向
如图所示,小朋友在玩一种运动中投掷的游戏,目的是在运动中将手中的球投进离地面高3m的吊环,他在车上和车一起以2m/s的速度向吊环运动,小朋友抛球时手离地面1.2m,当他在离吊环的水平距离为2m时将球相对于自己竖直上抛,球刚好进入吊环,他将球竖直向