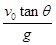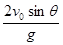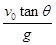题目内容
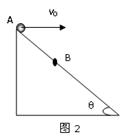
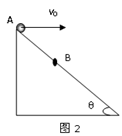
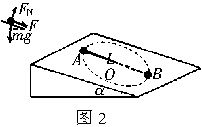
如图2所示,在倾角α=30°的光滑斜面上,有一根长L=0.8m的细绳,其一端固定在O点,另一端系一质量m=0.2kg的小球,沿斜面做圆周运动.试计算小球通过最高点A的最小速度.
2m/s
【试题分析】
【解析】小球在斜面上受到了重力、支持力和拉力三个力的作用,但支持力不改变小球的运动状态,小球在斜面上做圆周运动所需的向心力是由绳子的拉力和重力沿斜面方向的分力提供.小球的重力加速度沿斜面方向的分量为g'=gsinα.因此可将小球沿光滑斜面的运动看作是在重力加速度下的类似重力场中,沿竖直平面的圆周运动.根据模型1可知,小球通过最高点A的最小速度为
v最小=
 =2m/s
=2m/s小球在最低点B时,对绳子的拉力最大,所以绳子的抗拉能力至少应为
F最小=6mg'=6mgsin30°=6N

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
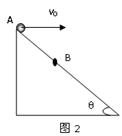
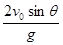 B、
B、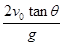 C、
C、 D、
D、