题目内容
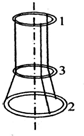
如图所示,三根不可伸长的相同的轻绳,一端系在半径为R的环1上,彼此间距相等.绳穿过半径为R的第3个圆环,另一端用同样方式系在半径为2R的圆环2上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离.(三个环都是用同种金属线制作的,摩擦不计)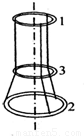
【答案】分析:根据环2环3的半径推知两者的质量关系,从而可知环1与环3之间每根绳的张力大小,因没有摩擦,绳子的重力不计,可知每根绳子沿其整个长度上的张力是相同的.再以环3为研究对象,对其受力分析,由平衡列式结合结合关系可得结果.
解答: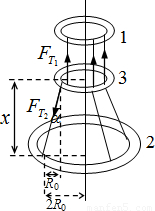 解:因为环2的半径为环3的2倍,环2的周长为环3的2倍,三环又是用同种金属丝制成的,所以环2的质量为环3的2倍.设m为环3的质量,那么三根绳承担的力为3mg,于是,环1与环3之间每根绳的张力FT1=mg.没有摩擦,绳的重量不计,故每根绳子沿其整个长度上的张力是相同的,
解:因为环2的半径为环3的2倍,环2的周长为环3的2倍,三环又是用同种金属丝制成的,所以环2的质量为环3的2倍.设m为环3的质量,那么三根绳承担的力为3mg,于是,环1与环3之间每根绳的张力FT1=mg.没有摩擦,绳的重量不计,故每根绳子沿其整个长度上的张力是相同的,
FT1=FT2=mg
对环2,平衡时有:2mg-3FT2cosα=0,
由此cosα= .
.
环2中心与环3中心之距离:
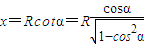
得:x=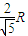
点评:对于有几个物体的相联力学问题,首先应用整体法确定某些物理量,若是不能达到求解目的时,再根据题设条件,应用隔离法,选取与所求物理量相关的物体为研究对象进行研究或分析,进而达到求解的目的.本题应用隔离法时选取环3为研究对象,后选环2为研究对象,分别求解,显然选环2为研究对象时的解答直观、简单,因为环2受力比环3少,在应用隔离法研究对象时往往是选择受力个数少而与求解物理量相关的物体为研究对象.
解答:
 解:因为环2的半径为环3的2倍,环2的周长为环3的2倍,三环又是用同种金属丝制成的,所以环2的质量为环3的2倍.设m为环3的质量,那么三根绳承担的力为3mg,于是,环1与环3之间每根绳的张力FT1=mg.没有摩擦,绳的重量不计,故每根绳子沿其整个长度上的张力是相同的,
解:因为环2的半径为环3的2倍,环2的周长为环3的2倍,三环又是用同种金属丝制成的,所以环2的质量为环3的2倍.设m为环3的质量,那么三根绳承担的力为3mg,于是,环1与环3之间每根绳的张力FT1=mg.没有摩擦,绳的重量不计,故每根绳子沿其整个长度上的张力是相同的,FT1=FT2=mg
对环2,平衡时有:2mg-3FT2cosα=0,
由此cosα=
 .
.环2中心与环3中心之距离:
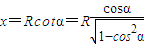
得:x=
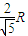
点评:对于有几个物体的相联力学问题,首先应用整体法确定某些物理量,若是不能达到求解目的时,再根据题设条件,应用隔离法,选取与所求物理量相关的物体为研究对象进行研究或分析,进而达到求解的目的.本题应用隔离法时选取环3为研究对象,后选环2为研究对象,分别求解,显然选环2为研究对象时的解答直观、简单,因为环2受力比环3少,在应用隔离法研究对象时往往是选择受力个数少而与求解物理量相关的物体为研究对象.

练习册系列答案
相关题目
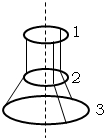 如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第2个圆环,另一端用同样方式系在半径为2R0的圆环3上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离及每根细绳的弹力(三个环都是用同种金属线制作的,摩擦不计)
如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第2个圆环,另一端用同样方式系在半径为2R0的圆环3上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离及每根细绳的弹力(三个环都是用同种金属线制作的,摩擦不计)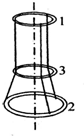 如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第3个圆环,另一端用同样方式系在半径为2R0的圆环2上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离.(三个环都是用同种金属线制作的,摩擦不计)
如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第3个圆环,另一端用同样方式系在半径为2R0的圆环2上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离.(三个环都是用同种金属线制作的,摩擦不计)
 如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第3个圆环,另一端用同样方式系在半径为2R0的圆环2上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离.(三个环都是用同种金属线制作的,摩擦不计)
如图所示,三根不可伸长的相同的轻绳,一端系在半径为R0的环1上,彼此间距相等.绳穿过半径为R0的第3个圆环,另一端用同样方式系在半径为2R0的圆环2上.环1固定在水平面上,整个系统处于平衡.试求第2个环中心与第3个环中心的距离.(三个环都是用同种金属线制作的,摩擦不计)