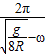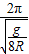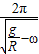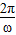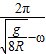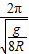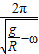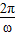题目内容
有一绕地球做匀速圆周运动的人造卫星,其运动方向与地球的自转方向相同.轨道半径为2R(R为地球半径).地球自转的角速度为ω0.若某时刻卫星经过赤道上某幢楼房的上空,那么卫星再次经过这幢楼房的上空时,需经历的时间为(已知地球表面的重力加速度为g)( )
分析:根据人造卫星的万有引力等于向心力,列式求出角速度的表达式,卫星再次经过这幢楼房的上空,地球多转动一圈.
解答:解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,有
F=F向
F=G
F向=mω2r
因而
G
=mω2r
解得
ω=
=
①
卫星再次经过这幢楼房的上空,卫星多转动一圈,有
(ω-ω0)t=2π ②
地球表面的重力加速度为
g=
③
联立①②③后,解得
t=
故选A.
F=F向
F=G
| Mm |
| r2 |
F向=mω2r
因而
G
| Mm |
| r2 |
解得
ω=
|
|
卫星再次经过这幢楼房的上空,卫星多转动一圈,有
(ω-ω0)t=2π ②
地球表面的重力加速度为
g=
| GM |
| R2 |
联立①②③后,解得
t=
| 2π | ||||
|
故选A.
点评:本题关键:(1)根据万有引力提供向心力求解出角速度;(2)根据地球表面重力等于万有引力得到重力加速度表达式;(3)根据多转动一圈后再次到达城市上空列式.

练习册系列答案
相关题目
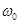 。若某时刻卫星正经过赤道上某幢楼房的正上方,那么卫星第二次经过这幢楼房正上方所需时间为 ▲ 。
。若某时刻卫星正经过赤道上某幢楼房的正上方,那么卫星第二次经过这幢楼房正上方所需时间为 ▲ 。