题目内容
(1)两磁铁各固定在一辆小车上,小车能在水平面上无摩擦地沿一直线运动,已知甲车和磁铁的总质量为0.5kg,乙车和磁铁的总质量为1.0kg,两磁铁的N极相对,推动一下,使两车相向运动,某时刻甲车的速度大小是2m/s,乙车的速度大小为3m/s,且仍在相向运动,则两车的距离最近时,乙车的速度大小为 m/s;甲车速度为零时,乙车的速度大小为 m/s.(2)我国2010年10月1号成功发射了探月卫星“嫦娥二号”.嫦娥二号卫星绕月工作轨道可近似看作圆轨道,已知其轨道高度为h,运行周期为T,月球平均半径为R,则嫦娥二号卫星绕月运行的加速度大小为 ,月球表面的重力加速度大小为 .
【答案】分析:(1)两车只有相互的磁力作用,不受外力,故动量守恒;而两车最近时,两车的速度相等;则由动量守恒可求得乙车的速度;
(2)已知嫦娥二号的周期、半径则可由a=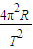 可求得求嫦娥二号的加速度;月球表面万有引力充当重力,可求得月球表面的重力加速度.
可求得求嫦娥二号的加速度;月球表面万有引力充当重力,可求得月球表面的重力加速度.
解答:解:(1)两车最近时,两车的速度相等,设乙车的速度为正方向,则由动量守恒可知:
m甲v甲+m乙v乙=(m甲+m乙)v
代入数据可得:
-0.5×2+1×3=(0.5+1)v
解得:v= m/s;
m/s;
当甲车速度为零时,由动量守恒可知:
m甲v甲+m乙v乙=m乙v′乙
解得:v′乙=2m/s;
故答案为: ;2.
;2.
(2)由a=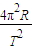 可知:
可知:
a=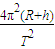
由万有引力公式可得:
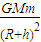 =m
=m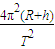
而月球表面的物体有:
 =mg
=mg
则可得g=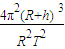
故答案为: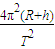 ;
;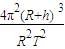
点评:本题的第一小题考查动量守恒定律的应用,注意分析运动的过程,明确相距最近应是速度相等时候;第二小问注意万有引力公式的应用即可.
(2)已知嫦娥二号的周期、半径则可由a=
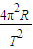 可求得求嫦娥二号的加速度;月球表面万有引力充当重力,可求得月球表面的重力加速度.
可求得求嫦娥二号的加速度;月球表面万有引力充当重力,可求得月球表面的重力加速度.解答:解:(1)两车最近时,两车的速度相等,设乙车的速度为正方向,则由动量守恒可知:
m甲v甲+m乙v乙=(m甲+m乙)v
代入数据可得:
-0.5×2+1×3=(0.5+1)v
解得:v=
 m/s;
m/s;当甲车速度为零时,由动量守恒可知:
m甲v甲+m乙v乙=m乙v′乙
解得:v′乙=2m/s;
故答案为:
 ;2.
;2.(2)由a=
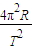 可知:
可知:a=
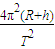
由万有引力公式可得:
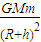 =m
=m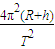
而月球表面的物体有:
 =mg
=mg则可得g=
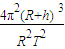
故答案为:
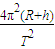 ;
;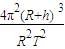
点评:本题的第一小题考查动量守恒定律的应用,注意分析运动的过程,明确相距最近应是速度相等时候;第二小问注意万有引力公式的应用即可.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目