题目内容
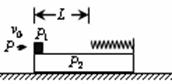
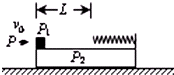 如图,一块平板P2置于光滑水平面上,质量为2m,其右端固定一轻质弹簧,左端放置一个物体P1,质量为m可看作质点.平板P2上弹簧的自由端离物体P1相距为L的部分是粗糙的,其余部分是光滑,且P1与P2之间的动摩擦因数为μ.现有一颗子弹P质量为
如图,一块平板P2置于光滑水平面上,质量为2m,其右端固定一轻质弹簧,左端放置一个物体P1,质量为m可看作质点.平板P2上弹簧的自由端离物体P1相距为L的部分是粗糙的,其余部分是光滑,且P1与P2之间的动摩擦因数为μ.现有一颗子弹P质量为| m | 2 |
(1)子弹P打入物体P1后的共同速度v1
(2)若子弹P与物体P1最终能停在平板P2的最左端,则L至少为多少?
(3)试讨论动摩擦因数为μ与此过程中弹簧的最大弹性势能EP 的关系.
分析:(1)子弹P打入物体P1后的共同速度根据系统的动量守恒定律求解.
(2)物体P1在物体P2并上滑过程中,系统的动量守恒,子弹P与物体P1最终能停在平板P2的最左端时,P1、P2、P三者速度相同,根据动量守恒定律求出共同速度,再根据能量守恒列式求解.
(3)当弹簧压缩最大时,P1、P2、P三者具有共同速度v3,由动量守恒定律和能量守恒定律求解.
(2)物体P1在物体P2并上滑过程中,系统的动量守恒,子弹P与物体P1最终能停在平板P2的最左端时,P1、P2、P三者速度相同,根据动量守恒定律求出共同速度,再根据能量守恒列式求解.
(3)当弹簧压缩最大时,P1、P2、P三者具有共同速度v3,由动量守恒定律和能量守恒定律求解.
解答:解:(1)子弹P打入P1过程,由于时间极短,P1所受的摩擦力冲量可忽略不计,P和P1组成的系统动量守恒.取向右方向为正方向,根据动量守恒定律得:
mv0=(
m+m)v1…①
解得:v1=
…②
(2)对P1、P2、P系统,所受的合外力为零,满足动量守恒,取向右方向为正方向.由动量守恒定律得:
mv1=(
m+2m)v2…③
解得:v2=
v1=
v0 ④
对系统由能量守恒定律得:
2μ(
m)g?L=
?
m
-
?(
m+2m)
…⑤
解得:L=
…⑥
(3)由系统的能量守恒定律:Ep=
?
m
-
?(
m+2m)
-μ(
m)g?L…⑦
当Ep=0时,由②④⑦得,μ=
.
若μ≥
时,Ep=0,
若μ<
时,Ep=
mv
-
μmgL
答:(1)子弹P打入物体P1后的共同速度v1为
.
(2)若子弹P与物体P1最终能停在平板P2的最左端,则L至少为
.
(3)动摩擦因数μ与此过程中弹簧的最大弹性势能EP的关系为:
若μ≥μ0=
时,Ep=0,
若μ<μ0=
时,Ep=
mv
-
μmgL.
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=
| v0 |
| 3 |
(2)对P1、P2、P系统,所受的合外力为零,满足动量守恒,取向右方向为正方向.由动量守恒定律得:
| 3 |
| 2 |
| 3 |
| 2 |
解得:v2=
| 3 |
| 7 |
| 1 |
| 7 |
对系统由能量守恒定律得:
2μ(
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 3 |
| 2 |
| v | 2 2 |
解得:L=
| ||
| 63μg |
(3)由系统的能量守恒定律:Ep=
| 1 |
| 2 |
| 3 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 3 |
| 2 |
| v | 2 2 |
| 3 |
| 2 |
当Ep=0时,由②④⑦得,μ=
2
| ||
| 63gL |
若μ≥
2
| ||
| 63gL |
若μ<
2
| ||
| 63gL |
| 1 |
| 21 |
2 0 |
| 3 |
| 2 |
答:(1)子弹P打入物体P1后的共同速度v1为
| v0 |
| 3 |
(2)若子弹P与物体P1最终能停在平板P2的最左端,则L至少为
| ||
| 63μg |
(3)动摩擦因数μ与此过程中弹簧的最大弹性势能EP的关系为:
若μ≥μ0=
2
| ||
| 63gL |
若μ<μ0=
2
| ||
| 63gL |
| 1 |
| 21 |
2 0 |
| 3 |
| 2 |
点评:本题综合考查了动量守恒定律、能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.对于多个相互作用的物体,往往优先考虑能否运用守恒定律求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
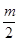 以速度
以速度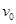 水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求
水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求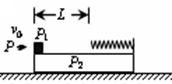
 以速度
以速度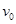 水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求
水平向右打入物体P1并留在其中,子弹打入过程时间极短。随后的运动过程中,(重力加速度为g)求


 本身不是易裂变材料,但是一种增殖材料,它能够吸收慢中子变成
本身不是易裂变材料,但是一种增殖材料,它能够吸收慢中子变成 ,然后经过________次________衰变转变为易裂变材料铀的同位素
,然后经过________次________衰变转变为易裂变材料铀的同位素 .
.