题目内容
如图甲所示,光滑、绝缘的直角三角形斜面MON固定在水平地面上,ON边长s=12m,θ=37°;虚线左、右空间分别存在磁感应强度为B1=
T,B2=
T的匀强磁场,方向分别垂直于纸面向外、向里;整个空间存在着竖直方向的、随时间交替变化的匀强电场(如图乙所示,竖直向上方向为正方向).在距O点为L=
处的P点有一物块抛射器,在t=0时刻将一质量为m、带电荷量为q(q>0)的小物块(可视为质点)抛入电磁场,小物块恰好能在0点切人ON斜面.设小物块在ON面上滑行时无电荷损失且所受洛伦兹力小于2mgcosθ,取g=10m/s?,求:

(1)小物块被抛出时的速度大小和方向.
(2)小物块从抛出到运动至N点所用的时间.
| 2πm |
| q |
| 4πm |
| q |
| 6 |
| π |

(1)小物块被抛出时的速度大小和方向.
(2)小物块从抛出到运动至N点所用的时间.
分析:(1)在t=0时刻小物块进入电磁场,由乙图知,电场方向向上,且有qE=mg,即电场力与重力平衡,则小物块在洛伦兹力作用下做匀速圆周运动,小物块要恰好能在0点切人ON斜面,被抛出时的速度方向必垂直于MO.由洛伦兹力提供向心力,由牛顿第二定律列式求速度的大小.
(2)分析小物块的运动情况,分段求时间.先做匀速圆周运动,运动半个周期,由T=
,t1=
求得时间t1;
小物块切入ON时,电场方向变为向下,沿斜面斜面做匀加速直线运动;当电场变为竖直向上后小物块正好做一个完整的圆周运动,然后电场方向又变为竖直向下,小物块继续沿斜面匀加速运动下滑,根据运动学公式和圆周运动的周期求总时间.
(2)分析小物块的运动情况,分段求时间.先做匀速圆周运动,运动半个周期,由T=
| 2πR |
| v |
| T |
| 2 |
小物块切入ON时,电场方向变为向下,沿斜面斜面做匀加速直线运动;当电场变为竖直向上后小物块正好做一个完整的圆周运动,然后电场方向又变为竖直向下,小物块继续沿斜面匀加速运动下滑,根据运动学公式和圆周运动的周期求总时间.
解答:解:(1)t=0时刻小物块进入电磁场,由乙图知,电场方向向上,且有qE=mg,所以小物块在洛伦兹力作用下做匀速圆周运动
小物块恰好由O点切入斜面,小物块被抛出时的速度方向必垂直于MO,设此过程中
小物块运动的时间为t1,有qvB=m
,T=
又R=
L,t1=
代入数据解得,小物块的抛出速度的大小v=6m/s,运动周期T=1s,在磁场B1中运动
的时间 t1=0.5s
(2)小物块切入ON时,电场方向变为向下,有(mg+qE)sinθ=ma
将 E=
代入,
解得 a=12m/s2
当电场变为竖直向上后小物块正好做一个完整的圆周运动,然后电场方向又变为竖直向下,小物块继续沿斜面以a=12m/s2的加速度下滑,故设小物块在斜面上滑行的总时间为t2,则有 s=vt2+
a
代入数据得 t2=1s,(t2=-2s舍去)
分析知,小物块沿斜面下滑0.5s后,作一个完整的圆周运动,然后又沿斜面下滑0.5s到达N点,设做圆周动动的时间是t3,
因为T=
,T′=
又B2=2B1,
所以 T=
T′,则t3=T=
T′=0.5s
小物块从P点运动到N点所用时间为t=t1+t2+t3=2s
答:
(1)小物块被抛出时的速度大小为6m/s,方向垂直于MO.
(2)小物块从抛出到运动至N点所用的时间是2s.
小物块恰好由O点切入斜面,小物块被抛出时的速度方向必垂直于MO,设此过程中
小物块运动的时间为t1,有qvB=m
| v2 |
| R |
| 2πR |
| v |
又R=
| 1 |
| 2 |
| T |
| 2 |
代入数据解得,小物块的抛出速度的大小v=6m/s,运动周期T=1s,在磁场B1中运动
的时间 t1=0.5s
(2)小物块切入ON时,电场方向变为向下,有(mg+qE)sinθ=ma
将 E=
| mg |
| q |
解得 a=12m/s2
当电场变为竖直向上后小物块正好做一个完整的圆周运动,然后电场方向又变为竖直向下,小物块继续沿斜面以a=12m/s2的加速度下滑,故设小物块在斜面上滑行的总时间为t2,则有 s=vt2+
| 1 |
| 2 |
| t | 2 2 |
代入数据得 t2=1s,(t2=-2s舍去)
分析知,小物块沿斜面下滑0.5s后,作一个完整的圆周运动,然后又沿斜面下滑0.5s到达N点,设做圆周动动的时间是t3,
因为T=
| 2πm |
| qB1 |
| 2πm |
| qB2 |
又B2=2B1,
所以 T=
| 1 |
| 2 |
| 1 |
| 2 |
小物块从P点运动到N点所用时间为t=t1+t2+t3=2s
答:
(1)小物块被抛出时的速度大小为6m/s,方向垂直于MO.
(2)小物块从抛出到运动至N点所用的时间是2s.
点评:解决本题的关键是分析物块的受力情况,判断其运动情况,逐段求解时间,从而得到总时间.

练习册系列答案
相关题目
 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.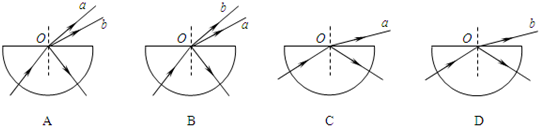
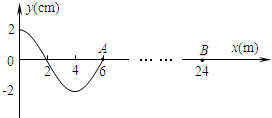
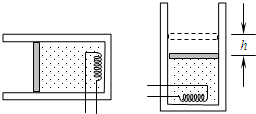
 如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )
如图甲所示,内壁光滑的绝热气缸竖直立于地面上,绝热活塞将一定质量的气体封闭在气缸中,活塞静止时处于A位置.现将一重物轻轻地放在活塞上,活塞最终静止在如图乙所示的B位置.设分子之间除相互碰撞以外的作用力可忽略不计,则活塞在B位置时与活塞在A位置时相比较( )

 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.

