题目内容
如图，质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端，OA和OB的长度均为l，可绕过O点且与纸面垂直的水平轴无摩擦转动，空气阻力不计．设A球带正电，B球带负电，电量均为q，处在竖直向下的匀强电场中，场强大小为E=| mg |
| q |
37°
37°
时A球具有最大速度，最大速度为
|
|
分析：小球A速度最大时，系统力矩处于平衡状态，根据力矩平衡方程可以求得平衡时小球所处于位置，即OA与竖直方向的夹角，根据动能定理，开始到小球速度最大的过程中，合外力对小系统所做的总功等于系统动能的增量．由此可以算出小球在速度最大时所具有的速度．
解答：解：（1）由题意知A和B的速度大小相等，当A球速度最大时，A和B及轻杆处于力矩平衡状态，如下图可知，此时OA杆与水平方向夹角为θ，当A球速度最大时，满足力矩平衡即：
FAlcosθ+GAlcosθ+FBlsinθ=GBlsinθ ①
FA=FB=qE=mg ②
由①②解得tanθ=
，即θ=53°
因为OA与水平方向成53°角，所以此时OA与竖直方向成37°角；
（2）因为AB速度始终相等，则从开始到速度最大时，对系统用动能定理有：
WFA+WGA+WGB+WFB=
(mA+mB)v2-0
又：WFA=qElsinθ，WGA=mglsinθ，WGB=-2mglcosθ，WFB=mglcosθ
代入E=
有：
mglsinθ+mglsinθ+（-2mglcosθ）+mglcosθ=
×
mv2
又θ=53°
所以：
+
-
+
=
mgl=
即v=
故答案为：37°，
FAlcosθ+GAlcosθ+FBlsinθ=GBlsinθ ①
FA=FB=qE=mg ②
由①②解得tanθ=
| 4 |
| 3 |
因为OA与水平方向成53°角，所以此时OA与竖直方向成37°角；
（2）因为AB速度始终相等，则从开始到速度最大时，对系统用动能定理有：
WFA+WGA+WGB+WFB=
| 1 |
| 2 |
又：WFA=qElsinθ，WGA=mglsinθ，WGB=-2mglcosθ，WFB=mglcosθ
代入E=
| mg |
| q |
mglsinθ+mglsinθ+（-2mglcosθ）+mglcosθ=
| 1 |
| 2 |
| 7 |
| 2 |
又θ=53°
所以：
| 4mgl |
| 5 |
| 4mgl |
| 5 |
| 6mgl |
| 5 |
| 3mgl |
| 5 |
| 7mv2 |
| 4 |
mgl=
| 7mv2 |
| 4 |
即v=
|
故答案为：37°，
|
点评：正确的理解力矩平衡，并能根据力矩平衡条件列出平衡方程是解决第一问的关键，在第二问中根据动能定理，合外力对系统做的总功等于系统动能的增量，以求最大速度变为求最大动能．
练习册系列答案
阅读快车系列答案
相关题目
如图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间的距离为L．已知A、B的中心和O三点始终共线，A和B分别在O的两侧．引力常数为G．求两星球做圆周运动的周期．
如图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动，星球A和B两者中心之间距离为L．已知A、B的中心和O三点始终共线，A和B分别在O的两侧．引力常数为G．
如图，质量分别为m和2.5m的两个小球A、B固定在弯成90°角的绝缘轻杆两端，OA和OB的长度均为l，可绕过O点且与纸面垂直的水平轴无摩擦转动，空气阻力不计．设A球带正电，B球带负电，电量均为q，处在竖直向下的匀强电场中，场强大小为E=mg/q．开始时，杆OA水平，由静止释放．求：
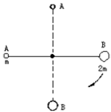如图，质量分别为m和2m的两个小球A和B，中间用轻质杆相连，在杆的中点O处有一固定转动轴，把杆置于水平位置后释放，在B球顺时针摆动到最低位置的过程中（ ）| A、杆对球的力沿杆方向 | B、杆对A球做正功，杆对B球做负功 | C、A球、B球、杆和地球组成的系统机械能守恒 | D、重力对A球做功的瞬时功率一直变大 |