题目内容
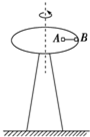 (2010?苏州二模)如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动.转台的同一半径上放有质量均为0.4kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.
(2010?苏州二模)如图所示,水平转台高1.25m,半径为0.2m,可绕通过圆心处的竖直转轴转动.转台的同一半径上放有质量均为0.4kg的小物块A、B(可看成质点),A与转轴间距离为0.1m,B位于转台边缘处,A、B间用长0.1m的细线相连,A、B与水平转台间最大静摩擦力均为0.54N,g取10m/s2.(1)当转台的角速度达到多大时细线上出现张力?
(2)当转台的角速度达到多大时A物块开始滑动?
(3)若A物块恰好将要滑动时细线断开,此后转台保持匀速转动,求B物块落地瞬间A、B两物块间的水平距离.(不计空气阻力,计算时取π=3)
分析:当转台的角速度比较小时,A、B物块做圆周运动的向心力由静摩擦力提供,随着角速度增大,由Fn=mω2r知向心力增大,由于B物块的转动半径大于A物块的转动半径,B物块的静摩擦力先达到最大静摩擦力,角速度再增大,则细线上出现张力,角速度继续增大,A物块受的静摩擦力也将达最大,这时A物块开始滑动.若A物块恰好将要滑动时细线断开,此后转台保持匀速转动,这时A物块在静摩擦力(小于最大静摩擦力)的作用下做匀速圆周运动,B物块沿切线方向飞出做平抛运动,然后,确定B平抛结束时A、B两物块的位置,进而求解A、B两物块间的水平距离.
解答:解:(1)、由Ff=mω2r可知随着角速度增大,向心力增大,由于B物块的转动半径大于A物块的转动半径,B物块的静摩擦力先达到最大静摩擦力,即B先达到临界状态,故当满足Ffm=mω12r时线上出现张力.
解得角速度:ω1=
=
rad/s=
rad/s.
(2)、当ω继续增大,A受静摩擦力也达到最大静摩擦力时,A开始滑动,设这时的角速度为ω′,
对A物块有:Ffm-FT=
r,
对B物块有:Ffm+FT=mω′2r,
代入数据得角速度为:ω′=
=
rad/s=3 rad/s.
(3)、细线断开后,B沿水平切线方向飞出做平抛运动,
竖直方向由h=
gt2得平抛的时间:t=0.5 s.
平抛的初速度:vB=ω′r=3×0.2m/s=0.6 m/s,
可得B的水平射程;xB=vBt=0.5×0.6m=0.3 m.
细线断开后,A还随转台一起做匀速圆周运动,t时间转过角度:
θ=ωt=1.5 rad,即90°,
故AB间水平距离:
lx=
=0.28 m.
答:(1)、当转台的角速度达到
rad/s时细线上出现张力.
(2)、当转台的角速度达到3rad/s时A物块开始滑动.
(3)、若A物块恰好将要滑动时细线断开,此后转台保持匀速转动,B物块落地瞬间A、B两物块间的水平距离是0.28m.
解得角速度:ω1=
|
|
3
| ||
| 2 |
(2)、当ω继续增大,A受静摩擦力也达到最大静摩擦力时,A开始滑动,设这时的角速度为ω′,
对A物块有:Ffm-FT=
| mω′ 2 |
| 2 |
对B物块有:Ffm+FT=mω′2r,
代入数据得角速度为:ω′=
|
|
(3)、细线断开后,B沿水平切线方向飞出做平抛运动,
竖直方向由h=
| 1 |
| 2 |
平抛的初速度:vB=ω′r=3×0.2m/s=0.6 m/s,
可得B的水平射程;xB=vBt=0.5×0.6m=0.3 m.
细线断开后,A还随转台一起做匀速圆周运动,t时间转过角度:
θ=ωt=1.5 rad,即90°,
故AB间水平距离:
lx=
(xB-
|
答:(1)、当转台的角速度达到
3
| ||
| 2 |
(2)、当转台的角速度达到3rad/s时A物块开始滑动.
(3)、若A物块恰好将要滑动时细线断开,此后转台保持匀速转动,B物块落地瞬间A、B两物块间的水平距离是0.28m.
点评:本题的关键是抓住临界状态,隔离物体,正确受力分析,在求水平位移时,一定搞清空间位置.

练习册系列答案
相关题目
 (2010?苏州二模)某同学用伏安法测一节干电池的电动势和内阻,现备有下列器材:
(2010?苏州二模)某同学用伏安法测一节干电池的电动势和内阻,现备有下列器材: (2010?苏州二模)如图所示,一质量m=0.20kg的物体,在F1、F2两水平力作用下静止在粗糙的水平面上.物体与水平面间的最大静摩擦力为O.6N.若F1为0.6N,则F2不可能是( )
(2010?苏州二模)如图所示,一质量m=0.20kg的物体,在F1、F2两水平力作用下静止在粗糙的水平面上.物体与水平面间的最大静摩擦力为O.6N.若F1为0.6N,则F2不可能是( ) (2010?苏州二模)如图是居民小区楼道灯通常采用的声、光控制节电开关电路图.白天的时候,即使拍手发出声音,灯也不亮;但到了晚上,声音达到一定强度,灯就亮了,并采用延时电路,使之亮了一段时间后熄灭.电路中K为声控开关,有声音时,电路接通.关于该电路,下列判断正确的是( )
(2010?苏州二模)如图是居民小区楼道灯通常采用的声、光控制节电开关电路图.白天的时候,即使拍手发出声音,灯也不亮;但到了晚上,声音达到一定强度,灯就亮了,并采用延时电路,使之亮了一段时间后熄灭.电路中K为声控开关,有声音时,电路接通.关于该电路,下列判断正确的是( ) (2010?苏州二模)如图所示,一理想变压器原、副线圈的匝数比n1:n2=4:1,电源电压U=220
(2010?苏州二模)如图所示,一理想变压器原、副线圈的匝数比n1:n2=4:1,电源电压U=220