题目内容
 如图,质量为m的物体置于倾角为θ的固定斜面上.物体与斜面之间的动摩擦因数为μ,先用平行于斜面的推力F1作用于物体上,使其能沿斜面匀速上滑,若改用水平推力F2作用于物体上,也能使物体沿斜面匀速上滑,则两次力之比
如图,质量为m的物体置于倾角为θ的固定斜面上.物体与斜面之间的动摩擦因数为μ,先用平行于斜面的推力F1作用于物体上,使其能沿斜面匀速上滑,若改用水平推力F2作用于物体上,也能使物体沿斜面匀速上滑,则两次力之比| F1 |
| F2 |
分析:以物体为研究对象,分析受力情况,作出力图,根据平衡条件运用正交分解法求解F1与F2的大小,再求它们的比值.
解答:解:F1作用时,物体的受力情况如图1,根据平衡条件得
F1=mgsinθ+μFN
FN=mgcosθ
解得:F1=mgsinθ+μmgcosθ
F2作用时,物体的受力情况如图2,根据平衡条件得
F2cosθ=mgsinθ+μFN′
FN′=mgcosθ+F2sinθ
解得:F2=
所以
=
=cosθ-μsinθ
故选B.

F1=mgsinθ+μFN
FN=mgcosθ
解得:F1=mgsinθ+μmgcosθ
F2作用时,物体的受力情况如图2,根据平衡条件得
F2cosθ=mgsinθ+μFN′
FN′=mgcosθ+F2sinθ
解得:F2=
| mgsinθ+μmgcosθ |
| cosθ-μsinθ |
所以
| F1 |
| F2 |
| mgsinθ+μmgcosθ | ||
|
故选B.
点评:本题是物体的平衡问题,受力分析,作出力图是正确解题的关键.中等难度.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
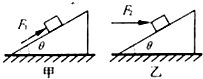 如图,质量为m的物体置于倾角θ=37°的固定斜面上,物体与斜面之间的动摩擦因数为μ=0.5,如图甲所示,先用平行于斜面的推力F1作用于物体上,能使其沿斜面匀速上滑,如图乙所示,若改用水平推力F2作用于物体上,也能使物体沿斜面匀速上滑,求:F1 与F2的比.
如图,质量为m的物体置于倾角θ=37°的固定斜面上,物体与斜面之间的动摩擦因数为μ=0.5,如图甲所示,先用平行于斜面的推力F1作用于物体上,能使其沿斜面匀速上滑,如图乙所示,若改用水平推力F2作用于物体上,也能使物体沿斜面匀速上滑,求:F1 与F2的比. 如图,质量为m的物体悬挂在轻质的支架上,斜梁OB与竖直方向的夹角为θ,设水平横梁OA和斜梁OB作用于O点的弹力分别为F1和F2.以下结果正确的是( )
如图,质量为m的物体悬挂在轻质的支架上,斜梁OB与竖直方向的夹角为θ,设水平横梁OA和斜梁OB作用于O点的弹力分别为F1和F2.以下结果正确的是( )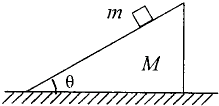 如图,质量为m的物体放在倾角为θ的斜面上并在下列过程中始终相对于斜面静止.则下面的说法正确的是( )
如图,质量为m的物体放在倾角为θ的斜面上并在下列过程中始终相对于斜面静止.则下面的说法正确的是( ) 如图,质量为m的物体,在沿斜面向上的拉力F作用下,沿质量为M的斜面体匀速下滑,此过程中斜面体仍静止,则水平面对斜面( )
如图,质量为m的物体,在沿斜面向上的拉力F作用下,沿质量为M的斜面体匀速下滑,此过程中斜面体仍静止,则水平面对斜面( )