题目内容
8. 如图一矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动,右端通过电刷a,b与一平行水平金属板相连接.已知线圈匝数为N=10匝,线圈面积S=0.5m2,线圈匀速转动的转速为n=60r/min,线圈内阻不计,磁场的磁感应强度B=$\frac{10}{π}$(T).平行金属板板长l=0.1m,板间距离d=0.2m,求:
如图一矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动,右端通过电刷a,b与一平行水平金属板相连接.已知线圈匝数为N=10匝,线圈面积S=0.5m2,线圈匀速转动的转速为n=60r/min,线圈内阻不计,磁场的磁感应强度B=$\frac{10}{π}$(T).平行金属板板长l=0.1m,板间距离d=0.2m,求:(1)从图示时刻开始计时,写出矩形线圈中的电动势随时间变化的函数关系式?
(2)若某时刻一质量为m=1×10-3Kg、带电量为q=0.2C的正粒子,从板中央以v0=100m/s的初速度水平射入平行金属板间,假设粒子在穿越板间的极短时间内电压不变,不计粒子重力,则粒子在金属板间的最大偏转位移为多少?
分析 (1)由最大值表达式可求得感应电动势的最大值,再由瞬时表达式规律可求得瞬时值;
(2)当电压达最大值时,粒子在金属板间的偏移量达最大,由类平抛运动的规律可求得最大偏移量.
解答 解:(1)线圈的转速n=60r/min=1r/s;
角速度ω=2πn=2π(rad/s)
感应电动势的最大值Em=NBsω=10×$\frac{10}{π}$×0.5×2π=100V;
由图可知,由最大值开始计时,故瞬时表达式e=Emcosωt=100cos2πt;
(2)解:(1)带电粒子在平行极板方向做匀速直线运动,由L=${v}_{0}^{\;}t$可得:
t=$\frac{L}{{v}_{0}^{\;}}$=$\frac{0.1}{100}$=0.001s
当电压达最大值时,偏转位移最大;
由E=$\frac{U}{d}$,F=Eq,及F=ma可得a=$\frac{qU}{md}$=$\frac{100×0.2}{1×1{0}^{-3}×0.2}$=1×105m/${s}_{\;}^{2}$
带电粒子在竖直方向偏转位移y=$\frac{1}{2}{at}_{\;}^{2}$,代入数据可得y=$\frac{1}{2}$×1×105×(0.001)2=0.05m;
答:(1)矩形线圈中的电动势随时间变化的函数关系式为e=100cos2πt;
(2)粒子在金属板间的最大偏转位移为0.05m
点评 带电粒子在匀强电场中的偏转可以用类平抛规律求解,将带电粒子沿初速度方向和垂直初速度的方向分解,然后根据两分运动的独立性和等时性根据牛顿定律列式求解即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图所示.弹簧左端固定,右端自由伸长到O点并系住物体m.现将弹簧压缩到A点,然后释放,物体一直可以运动到B点.如果物体受到的阻力恒定,则( )
如图所示.弹簧左端固定,右端自由伸长到O点并系住物体m.现将弹簧压缩到A点,然后释放,物体一直可以运动到B点.如果物体受到的阻力恒定,则( )
 如图所示.弹簧左端固定,右端自由伸长到O点并系住物体m.现将弹簧压缩到A点,然后释放,物体一直可以运动到B点.如果物体受到的阻力恒定,则( )
如图所示.弹簧左端固定,右端自由伸长到O点并系住物体m.现将弹簧压缩到A点,然后释放,物体一直可以运动到B点.如果物体受到的阻力恒定,则( )| A. | 物体从A到O先加速后减速 | |
| B. | 物体从A到O加速运动,从O到B减速运动 | |
| C. | 物体运动到O点时所受合力为零 | |
| D. | 物体从A到O的过程加速度逐渐减小 |
19.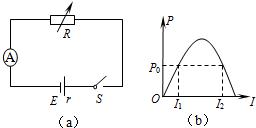 如图(a),R为电阻箱,A为理想电流表,电源的电动势为E,内阻为r.图(b)为电源的输出功率P与A示数I的关系图象,其中功率P0分别对应电流I1、I2.则( )
如图(a),R为电阻箱,A为理想电流表,电源的电动势为E,内阻为r.图(b)为电源的输出功率P与A示数I的关系图象,其中功率P0分别对应电流I1、I2.则( )
 如图(a),R为电阻箱,A为理想电流表,电源的电动势为E,内阻为r.图(b)为电源的输出功率P与A示数I的关系图象,其中功率P0分别对应电流I1、I2.则( )
如图(a),R为电阻箱,A为理想电流表,电源的电动势为E,内阻为r.图(b)为电源的输出功率P与A示数I的关系图象,其中功率P0分别对应电流I1、I2.则( )| A. | I1+I2>$\frac{E}{r}$ | B. | I1+I2<$\frac{E}{r}$ | C. | I1+I2=$\frac{E}{r}$ | D. | I1=I2=$\frac{E}{r}$ |
16.质量不等的两星体在相互间的万有引力作用下,绕两者连线上某一定点O做匀速圆周运动,构成双星系统.由天文观察测得其运动周期为T两星体之间的距离为r,已知引力常量为G.下列说法正确的是( )
| A. | 双星系统的平均密度为$\frac{3π}{{G{T^2}}}$ | |
| B. | O点离质量较大的星体较远 | |
| C. | 双星系统的总质量为$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | |
| D. | 若在O点放一物体,则物体受两星体的万有引力合力为零 |
9.下列说法正确的是( )
| A. | 变速直线运动的速度是变化的 | |
| B. | 平均速度即为速度的平均值 | |
| C. | 平均速率是平均速度的大小 | |
| D. | 瞬时速度可看作时间趋于无穷小时的平均速度 |
 如图所示,足够长的金属导轨MN、PQ平行放置,间距为L=0.5m,与水平面成θ=30°角,导轨与定值电阻R1和R2相连,且R1=R2=2Ω,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m=1.6kg、长度为L=0.5m、电阻为r=2Ω的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为v=2m/s,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.重力加速度g取10m/s2,导轨电阻不计,求:
如图所示,足够长的金属导轨MN、PQ平行放置,间距为L=0.5m,与水平面成θ=30°角,导轨与定值电阻R1和R2相连,且R1=R2=2Ω,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m=1.6kg、长度为L=0.5m、电阻为r=2Ω的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为v=2m/s,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.重力加速度g取10m/s2,导轨电阻不计,求: 如图所示,两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上,导轨间距为L,电阻忽略不计且足够长,以宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B.另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形线框连在一起组成的固定装置,总质量为m,导体棒中通有大小恒为I的电流.将整个装置置于导轨上,开始时导体棒恰好位于磁场的下边界处.由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度为g.
如图所示,两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上,导轨间距为L,电阻忽略不计且足够长,以宽度为d的有界匀强磁场垂直于斜面向上,磁感应强度为B.另有一长为2d的绝缘杆将一导体棒和一边长为d(d<L)的正方形线框连在一起组成的固定装置,总质量为m,导体棒中通有大小恒为I的电流.将整个装置置于导轨上,开始时导体棒恰好位于磁场的下边界处.由静止释放后装置沿斜面向上运动,当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零.重力加速度为g.