题目内容
 (2011?永春县模拟)某同学根据电磁感应现象设计了一种发电装置,如图甲所示,图乙为其俯视图.将8块相同磁铁的N、S极交错放置组合成一个高h=0.5m、半径r=0.2m的圆柱体,其可绕固定的OO'轴转动.圆柱外侧附近每个磁场区域的磁感应强度大小均为B=0.2T,方向都垂直于圆柱表面,相邻两个区域的磁场方向相反.紧靠圆柱体外侧固定-根与其等长、电阻R=0.4Ω的金属杆ab,杆与圆柱平行.从上往下看,圆柱体以ω=100rad/s的角速度顺时针匀速转动,设转到如图所示位置为t=0时刻.取g=10m/s2,π2=10.求:
(2011?永春县模拟)某同学根据电磁感应现象设计了一种发电装置,如图甲所示,图乙为其俯视图.将8块相同磁铁的N、S极交错放置组合成一个高h=0.5m、半径r=0.2m的圆柱体,其可绕固定的OO'轴转动.圆柱外侧附近每个磁场区域的磁感应强度大小均为B=0.2T,方向都垂直于圆柱表面,相邻两个区域的磁场方向相反.紧靠圆柱体外侧固定-根与其等长、电阻R=0.4Ω的金属杆ab,杆与圆柱平行.从上往下看,圆柱体以ω=100rad/s的角速度顺时针匀速转动,设转到如图所示位置为t=0时刻.取g=10m/s2,π2=10.求:(1)圆柱体转过周期的时间内,ab杆中产生的感应电动势E的大小;
(2)如图丙所示,M、N为水平放置的平行板电容器的两极板,极板长L0=0.314m,两板间距d=0.125m.现用两根引线将M、N分别与a、b相连.在t=0时刻,将-个电量q=+1.00×10-6C、质量m=1.60×10-8kg的带电粒子从紧靠M板中心处无初速度地释放,求粒子从M板运动到N板所经历的时间t.不计粒子重力.
(3)t=0时刻,在如图丙所示的两极板间,若上述带电粒子从靠近M板的左边缘处以初速度υ0水平射入两极板间,而且已知粒子沿水平方向离开电场,求初速度υ0的大小,并在图中画出粒子相应的运动轨迹.不计粒子重力.(※请自行作图!)
分析:(1)磁场与导体棒之间有相对运动,导体切割磁感线,根据E=BLv,即可求得ab杆中产生的感应电动势E的大小;
(2)粒子开始
T内做初速度为零的匀加速直线运动,然后减速
T,然后分别再加速、减速
T,这样往复下去,分析清楚运动过程,根据运动学公式和牛顿第二定律可求解;
(3)粒子最后以水平速度射出,说明粒子竖直方向上速度为零,因此粒子在板间运动时间为
T的偶数倍,即为
T或者
T.
(2)粒子开始
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
(3)粒子最后以水平速度射出,说明粒子竖直方向上速度为零,因此粒子在板间运动时间为
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 2 |
解答: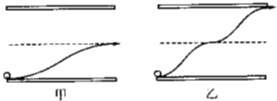 解:(1)感应电动势:E=Bhv
解:(1)感应电动势:E=Bhv
又:v=ωr
E=2V
代入数据得:故ab杆中产生的感应电动势E的大小为:E=2V
(2)粒子加速度为:a=
周期为:T=
粒子在
T时间内运动地距离为:so=
a(
T)2=
m
又:
=4
故:t=4×
=
T=3.14×10-2
故粒子从M板运动到N板所经历的时间t=3.14×10-2s.
(3)第一种情况:粒子运动轨迹如答图甲所示,运动时间为
T.
初速度应为:v01=
=20m/s
第二种情况:粒子运动轨迹如答图乙所示,运动时间为
T.
初速度应为:v02=
=10m/s
故初速度大小分别为20m/s,10m/s,轨迹如图所示.
 解:(1)感应电动势:E=Bhv
解:(1)感应电动势:E=Bhv又:v=ωr
E=2V
代入数据得:故ab杆中产生的感应电动势E的大小为:E=2V
(2)粒子加速度为:a=
| Uq |
| dm |
周期为:T=
| 2π |
| ω |
粒子在
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 32 |
又:
| d |
| so |
故:t=4×
| T |
| 8 |
| 1 |
| 2 |
故粒子从M板运动到N板所经历的时间t=3.14×10-2s.
(3)第一种情况:粒子运动轨迹如答图甲所示,运动时间为
| 1 |
| 4 |
初速度应为:v01=
| Lo | ||
|
第二种情况:粒子运动轨迹如答图乙所示,运动时间为
| 1 |
| 2 |
初速度应为:v02=
| l0 | ||
|
故初速度大小分别为20m/s,10m/s,轨迹如图所示.
点评:本题有一定的综合性,借助电磁感应考查了带电粒子在电场中的运动,注意分析清楚运动过程和运动的周期性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?永春县模拟)在做“研究匀变速直线运动”的实验中,取下一段如图所示的纸带研究其运动情况.设O点为计数的起始点,在四个连续的计数点中,相邻两计数点间的时间间隔为0.1s,若物体做理想的匀加速直线运动,则计数点A与起始点O之间的距离s1为
(2011?永春县模拟)在做“研究匀变速直线运动”的实验中,取下一段如图所示的纸带研究其运动情况.设O点为计数的起始点,在四个连续的计数点中,相邻两计数点间的时间间隔为0.1s,若物体做理想的匀加速直线运动,则计数点A与起始点O之间的距离s1为 (2011?永春县模拟)如图所示的电路中,电源的电动势为E,内阻为r.当可变电阻的滑片P向b移动时,电压表V1的示数U1与电压表V2的示数U2的变化情况是( )
(2011?永春县模拟)如图所示的电路中,电源的电动势为E,内阻为r.当可变电阻的滑片P向b移动时,电压表V1的示数U1与电压表V2的示数U2的变化情况是( ) (2011?永春县模拟)在做“测定金属的电阻率”的实验时,有位同学按图所示电路进行连线,他共用7根导线:ab、cd、ef、ff′、e′d′、d′c′、b′a′,由于其中有一根内部断开的导线,所以当他合上开关S后,无论怎样移动滑动变阻器的滑片,电压表读数都约为4.5V,电流表读数接近零.
(2011?永春县模拟)在做“测定金属的电阻率”的实验时,有位同学按图所示电路进行连线,他共用7根导线:ab、cd、ef、ff′、e′d′、d′c′、b′a′,由于其中有一根内部断开的导线,所以当他合上开关S后,无论怎样移动滑动变阻器的滑片,电压表读数都约为4.5V,电流表读数接近零.