题目内容
12. 一宇航员抵达半径为R的星球表面后,做了如下实验:取一细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直面内做匀速圆周运动,如图所示.观察测力计,当砝码运动到圆周的最低点时,读书为F1;当砝码运动到圆周的最高点时,读数为F2.求:在该星球表面发射人造卫星所需的第一宇宙速度.
一宇航员抵达半径为R的星球表面后,做了如下实验:取一细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直面内做匀速圆周运动,如图所示.观察测力计,当砝码运动到圆周的最低点时,读书为F1;当砝码运动到圆周的最高点时,读数为F2.求:在该星球表面发射人造卫星所需的第一宇宙速度.
分析 砝码在竖直平面内做匀速圆周运动,当砝码运动到圆周最低点和最高点时,根据牛顿第二定律列式求出重力加速度,从而求出第一宇宙速度.
解答 解:砝码在竖直平面内做匀速圆周运动,当砝码运动到圆周最低点时有:${F_1}-mg=m\frac{v^2}{R}$
当砝码运到到圆周的最高点时有:${F_2}+mg=m\frac{v^2}{R}$
联立两式解得:$g=\frac{{{F_1}-{F_2}}}{2m}$
在星球表面,万有引力近似等于重力,则有:mg=m$\frac{{v}^{2}}{R}$
该星球的第一宇宙速度为:$v=\sqrt{gR}=\sqrt{\frac{{({F_1}-{F_2})R}}{2m}}$
答:在该星球表面发射人造卫星所需的第一宇宙速度为$\sqrt{\frac{({F}_{1}-{F}_{2})R}{2m}}$.
点评 根据砝码做圆周运动时在最高点和最低点的运动规律,找出向心力的大小,可以求得重力加速度,
知道在星球表面时,万有引力和重力近似相等,而贴着星球的表面做圆周运动时,物体的重力就作为做圆周运动的向心力.

练习册系列答案
相关题目
2.关于密闭容器中气体的压强,下列说法正确的是( )
| A. | 气体压强是由于气体分子相互作用产生的 | |
| B. | 气体压强是由于大量气体分子频繁碰撞容器壁产生的 | |
| C. | 气体压强只跟气体分子分子的密集程度有关 | |
| D. | 在完全失重的情况下,密闭容器内的气体对器壁没有压强 |
3.一物块从某一高度水平抛出,刚抛出时其动能与重力势能恰好相等(取水平地面作为参考平面).不计空气阻力,该物块落地时的速度方向与水平方向的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
7.关于功率,下列说法中正确的是( )
| A. | 力对物体做功越多,则力做功的功率越大 | |
| B. | 从公式P=Fv可知,汽车的牵引力一定跟汽车行驶的速率成反比 | |
| C. | 由公式P=$\frac{W}{t}$可知,物体做功时间越短,其功率越大 | |
| D. | 功率是描述物体做功快慢的物理量 |
17.关于机械能守恒定律,正确的说法是( )
| A. | 只有当物体仅受重力作用时,机械能才守恒 | |
| B. | 只有当物体仅受弹簧的作用力时,机械能才守恒 | |
| C. | 只有弹簧的力对物体做功时,物体和地球的机械能守恒 | |
| D. | 若不计空气的阻力,则做平抛运动物体和地球组成的系统机械能守恒 |
4.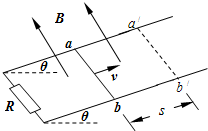 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感强度为B.有一质量为m长为l的导体棒从ab位置获平行斜面的大小为v的初速向上运动,最远到达虚线a′b′的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒受到的最大安培力为$\frac{{B}^{2}{l}^{2}v}{R}$ | |
| B. | 上滑过程中导体棒损失的机械能大小为μmgs cosθ | |
| C. | 上滑过程中电流做功发出的热量为$\frac{m{v}^{2}}{2}$-mgs (sinθ+μcosθ) | |
| D. | 上滑过程中安培力、滑动摩擦力和重力对导体棒做的总功为正$\frac{m{v}^{2}}{2}$ |
2.发现万有引力定律的物理学家是( )
| A. | 开普勒 | B. | 牛顿 | C. | 卡文迪许 | D. | 伽利略 |
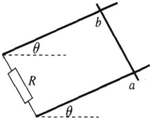 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(g取10rn/s2,sin37°=0.6,cos37°=0.8)
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.(g取10rn/s2,sin37°=0.6,cos37°=0.8)