题目内容
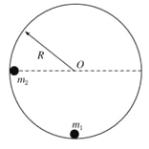
【题目】如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m 1 的小球静止在轨道最低点,另一质量为m2 的小球（两小球均可视为质点）从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1 发生碰撞并粘在一起.求
①小球m2 刚要与m1 发生碰撞时的速度大小;
②碰撞后,m1 和m2 能沿内壁运动所能达到的最大高度（相对碰撞点）
【答案】①
；②
【解析】
试题分析：（1）设小球m2运动到最低点时的速度为v0
由机械能守恒定律：
①
解得：
②
（2）设两球碰撞后，m1、m2两球粘在一起的速度为v，规定向右为正方向
m2v0=（m1+m2）v ③
设两球碰撞后上升的最大高度为h
（m1+m2）v2=（m1+m2）gh…④
解得：
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
