题目内容
如图所示，质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放，下摆后在最低点处与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用，金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘求偏离竖直方向的最大角度将小于45°。
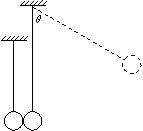
3次
解析:
绝缘球每次碰撞都要减少部分机械能，根据弹性碰撞过程中的动量守恒和机械能守恒可以求出碰后绝缘球的动能，从而得到碰撞次数。
解：设在第n次碰撞前绝缘球的速度为vn－1，碰撞后绝缘球、金属球的速度分别为vn、Vn。由于碰撞过程中动量守恒、碰撞前后动能相等，设速度向左，则
解得： 
第n次碰撞后绝缘球的动能为：
E0为第1次碰撞前的动能，即初始能量
绝缘球在θ＝θ0＝60°与θ＝45°处的势能之比为
经n次碰撞后有： 
易算出(0.81)2＝0656，(0.81)3＝0.531，因此，经过3次碰撞后θ小于45°
本题突出考查了发生弹性碰撞前后的动量守恒和动能守恒定律的掌握和运用，强调了数列的运算。由于现行教材和《考试大纲》都将弹性碰撞的相关计算删去了，所以一般学生都不知道弹性碰撞中动量和动能守恒公式，更谈不上记住它，因此解答此题很多学生是通过解二元二次方程组才得到答案的。本题运算量
练习册系列答案
相关题目
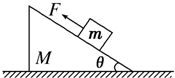如图所示，质量为M的斜面放置于水平面上，其上有质量为m的小物块，各接触面均无摩擦力，第一次将水平力F1加在M上，第二次将F2加在m上，两次都要求m与M不发生相对滑动，则F1与F2的比为（ ）
如图所示，质量为m的小球，距水平面高为2m时，速度的大小为4m/s，方向竖直向下，若球的运动中空气阻力的大小等于重力的0.1倍，与地面相碰的过程中不损失机械能，求：
如图所示，质量为m的小球，从A点由静止开始加速下落，加速度大小为
如图所示，质量为M的人通过定滑轮将质量为m的重物以加速度a上提，重物上升过程，人保持静止．若绳与竖直方向夹角为θ，求：
如图所示，质量为M的楔形物块静止在水平地面上，其斜面的倾角为θ．斜面上有一质量为m的小物块，小物块与斜面之间存在摩擦．用恒力F沿斜面向上拉，使之匀速上滑．在小物块运动的过程中，楔形物块始终保持静止，则（ ）| A、地面对楔形物块的支持力为（M+m）g | B、地面对楔形物块的摩擦力为零 | C、楔形物块对小物块摩擦力可能为零 | D、小物块一定受到四个力作用 |