题目内容
宇航员到了某星球后做了如下实验:如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ。当圆锥和球一起以周期T匀速转动时,球恰好对锥面无压力.已知星球的半径为R,万有引力常量为G.求: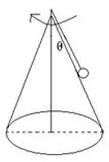
(1)线的拉力;
(2)该星球表面的重力加速度;
(3)该星球的第一宇宙速度;
(4)该星球的密度.
(1)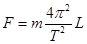 (2)
(2)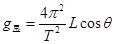
(3)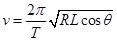 (4)
(4)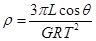
解析试题分析:(1)小球做圆周运动:向心力  ①(1分)
①(1分)
半径 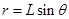 ②(1分)
②(1分)
解得线的拉力 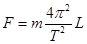 ③(1分)
③(1分)
(2)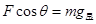 ④(1分)
④(1分)
解得该星球表面的重力加速度 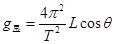 ⑤(2分)
⑤(2分)
(3)星球的第一宇宙速度即为该星球的近“地”卫星的环绕速度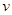 ,设近“地”卫星的质量为
,设近“地”卫星的质量为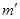 ,根据向心力公式有:
,根据向心力公式有: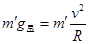 ⑥(1分)
⑥(1分)
联立⑤⑥解得 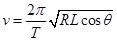 (2分)
(2分)
(4)设星球的质量为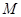 ,则:
,则: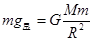 ⑦(1分)
⑦(1分) ⑧(1分)
⑧(1分)
联立⑤⑦⑧⑨解得星球的密度 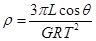 (1分)
(1分)
考点:万有引力定律 第一宇宙速度

练习册系列答案
相关题目
“神舟十号”飞船将于2013年6月至8月择机发射,再次与“天官一号”进行交会对接.三位航天员再次人住“天宫”完成一系列实验.“神舟十号”与“天宫一号”对接后做匀速圆周运动,运行周期为90分钟.对接后“天宫一号”的
| A.运行速度大于第一宇宙速度 |
| B.加速度大于赤道上静止物体随地球自转的加速度 |
| C.角速度为地球同步卫星角速度的16倍 |
| D.航天员可以用天平测出物体的质量 |
对下列物理现象的解释,正确的是( )
| A.击钉时,不用橡皮锤仅仅是因为橡皮锤太轻 |
| B.跳远时,在沙坑里填沙,是为了减小冲量 |
| C.易碎品运输时,要用柔软材料包装,船舷常常悬挂旧轮胎,都是为了延长作用时间,减小作用力 |
| D.在车内推车推不动,是因为合外力冲量为零 |
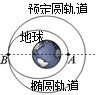
 变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点
变轨进入绕月飞行圆轨道;已知“嫦娥一号”绕月飞行的椭圆轨道远月点 距月球表面高度为
距月球表面高度为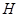 ;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为
;又已知“嫦娥一号”绕月圆轨道飞行时,距月球表面的高度为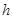 ,飞行周期为
,飞行周期为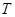 ,月球的半径为
,月球的半径为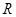 ,万有引力常量为
,万有引力常量为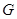 ;再后,假设宇航長在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为
;再后,假设宇航長在飞船上,操控飞船在月球表面附近竖直平面内俯冲,在最低点附近作半径为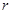 的圆周运动,宇航员质量是
的圆周运动,宇航员质量是 ,飞船经过最低点时的速度是
,飞船经过最低点时的速度是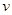 .求:
.求: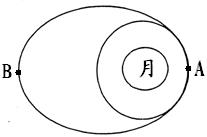
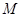 是多大?
是多大? 是多大?
是多大?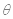 ,箱子做匀速直线运动.(引力常量为G)求:
,箱子做匀速直线运动.(引力常量为G)求: