Question

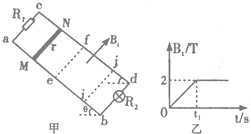如图甲所示凋足够长的平行光滑金属导轨ab、_Cd倾斜放置，两导轨之间的距离为 L=0.5m，导轨平面与水平面^间的夹角为θ=30°，导轨上端a、c之间连接有一阻值为R₁=4Ω的电阻，下端b、d之间接有一阻傳为R₂=4Ω的小灯泡．有理想边界的勻强磁场垂直于导轨平面向 上，虚线ef为磁场的上边序，ij为磁场的下边界，此区域内的感应强度B，随时间t变化的规律如图乙所示，现将一质量为m=

1

3

kg的金属棒MN，从距离磁场上边界ef的一定距离处，从t=0时刻开始由静止释放，金属棒MN从开始运动到经过磁场的下边界ij的过程中，小灯泡的亮度始终不变．金属棒MN在两轨道间的电阻r=1Ω，其余部分的电阻忽略不计，ef、ij边界均垂直于两导轨．重力 加速度g=10m/s²．求_：
（l）小灯泡的实际功率&
（2）金属棒MN穿出磁场前的最大速率；
（3）整个过程中小灯泡产生的热量．

Answer 1

分析：（1）由于小灯泡的亮度始终不变，说明金属棒MN进入磁场后做匀速直线运动，根据共点力平衡求出金属棒的电流的大小，结合功率的公式求出小灯泡的实际功率．
（2）根据闭合电路欧姆定律求出感应电动势的大小，结合切割产生的感应电动势公式求出金属棒MN穿出磁场前的最大速率．
（3）根据牛顿第二定律，结合运动学公式求出金属棒进入磁场前运动的时间，结合法拉第电磁感应定律和闭合电路欧姆定律求出磁场上下边界的长度，从而求出金属棒在磁场中运动的时间，结合Q=Pt求出整个过程中产生的热量．

解答：解：（1）由于小灯泡的亮度始终不变，说明金属棒MN进入磁场后做匀速直线运动，速度v达到最大，由平衡条件得：
mgsinθ=BIL
小灯泡的电功率为：P=(

I

2

)2R2
代入数据解得：P=

25

9

W．
（2）由闭合电路欧姆定律得：I=

E

R

其中，总电阻为：R=

R1

2

+r
由切割产生的感应电动势公式得：E=BLv
联立以上各式，代入数据解得v=5m/s．
（3）金属棒进入磁场前，由牛顿第二定律得：mgsinθ=ma
加速度为：a=gsin30°=5m/s²．
进入磁场前所用的时间为：t1=

v

a

设磁场区域的长度为x，在0-t₁时间内，
由法拉第电磁感应定律得：E′=

△Φ

△t

=

Lx(B-0)

t1

=

LxB

t1

．
金属棒MN进入磁场前，总电阻为：R=

R1r

R1+r

+R2
感应电动势为：E′=

I

2

R
在磁场中运动的时间为：t2=

x

v

整个过程中产生的热量为：Q=P（t₁+t₂）
代入数据解得：Q=5J．
答：（1）小灯泡的实际功率为

25

9

W．
（2）金属棒MN穿出磁场前的最大速率为5m/s．
（3）整个过程中小灯泡产生的热量为5J．

点评：本题考查了电磁感应与电路和力学和的综合，综合性较强，是高考常见的题型，在平时的学习中需加强训练．