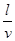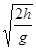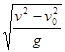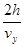题目内容
在倾角为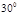 的光滑斜面上,一小球从A点由静止释放经时间
的光滑斜面上,一小球从A点由静止释放经时间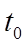 到达B点,另一个小球从A点水平抛出,落点也在B点,从以上情况可知( )
到达B点,另一个小球从A点水平抛出,落点也在B点,从以上情况可知( )
A.平抛小球运动时间也为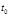 | B.平抛小球运动时间为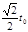 |
C.平抛小球的初速度为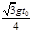 | D.平抛小球的初速度为 |
C
解析试题分析:小球从斜面滑下的加速度大小为a=gsin30°,S=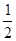 a
a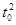 =
=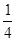 g
g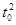
对于平抛运动的小球,设运动时间为t,则Ssin30°=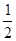 gt2,代入解得 t=
gt2,代入解得 t=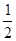 t0
t0
初速度 v0=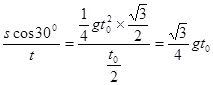 ,故选C
,故选C
考点:考查平抛运动规律
点评:本题难度较小,根据牛顿第二定律求出小球从斜面滑下的加速度,由位移求出A到B的位移大小.根据两球的位移相同,则可求出另一小球下落的高度.根据平抛运动竖直方向是自由落体运动,由高度求出时间.由水平方向的匀速运动,求出初速度

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图所示,P是水平面上的圆弧凹槽,从高台边B点以速度v0水平飞出的小球,恰能从固定在某位置的凹槽的圆弧轨道的左端A沿圆弧切线方向进入轨道。O是圆弧的圆心,θ1是OA与竖直方向的夹角,θ2是BA与竖直方向的夹角。则
A.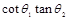 =2 =2 | B. =2 =2 |
C. =2 =2 | D. =2 =2 |
学校喷水池中的喷水口向两旁水平喷出,如图所示,若忽略空气阻力及水之间的相互作用,则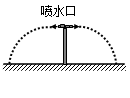
| A.喷水速度一定,喷水口越高,水喷得越远 |
| B.喷水速度一定,喷水口越高,水喷得越近 |
| C.喷水口高度一定,喷水速度越大,水喷得越远 |
| D.喷水口高度一定,喷水速度越大,水喷得越近 |
如图所示,具有圆锥形状的陀螺,半径为R,绕它的轴在光滑的桌面上以角速度 快速旋转,同时轴以速度v向左运动,若陀螺的轴一直保持竖直,为使陀螺从左侧桌子边缘滑出时不会与桌子边缘发生碰撞,v至少应等于
快速旋转,同时轴以速度v向左运动,若陀螺的轴一直保持竖直,为使陀螺从左侧桌子边缘滑出时不会与桌子边缘发生碰撞,v至少应等于
A. | B. |
C. | D. |
如图所示x轴在水平地面内,y轴沿竖直方向。图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则
| A.a的飞行时间比b的长 | B.b和c的飞行时间相同 |
| C.a的水平速度比b的小 | D.b的初速度比c的大 |
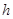 处以初速度
处以初速度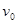 水平抛出,落地时速度为
水平抛出,落地时速度为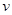 ,竖直分速度为vy,水平射程为
,竖直分速度为vy,水平射程为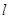 ,不计空气阻力,则物体在空中飞行的时间为
,不计空气阻力,则物体在空中飞行的时间为