题目内容
【题目】关于物体在斜面上的运动,请回答以下问题.已知最大静摩擦力等于滑动摩擦力.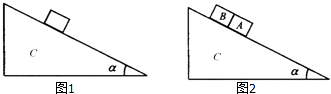
(1)如图1所示,一个截面为直角三角形的斜面体C始终静止在粗糙水平面上,物块能在C的斜面上保持静止,则物块与斜面之间的动摩擦因数μ与斜面倾角α应满足什么关系?
(2)如图2所示,两个质量均为m的小方块A和B紧挨着一起沿斜面体C的斜面匀速下滑,C始终静止在粗糙的地面上,A与B的接触面是光滑的.已知A与C之间的动摩擦因数是B与C之间动摩擦因数的2倍,斜面的倾角为α,求B与C之间的动摩擦因数为多少?
②接①问,若将A、B对调位置,再同时由静止释放A、B,发现C依然能保持在地面不动,若C的质量为M,求C与地面之间的动摩擦因数应满足的条件.
【答案】
(1)
解:物块能在C的斜面上保持静止,则应满足:mgsinα≤μmgcosα
可得 μ≥tanα
(2)
解:设B与C之间的动摩擦因数为μ1,则A与C之间的动摩擦因数是2μ1.
A、B一起沿斜面体C的斜面匀速下滑时,则有:
2mgsinα=μ1mgcosα+2μ1mgcosα
则:μ1= ![]()
若将A、B对调位置,对A,由于2μ1mgcosα= ![]() mgsinα>mgsinα,故A静止在C上.
mgsinα>mgsinα,故A静止在C上.
对B,由于μ1mgcosα= ![]() mgsinα<mgsinα,故B在C上下滑.
mgsinα<mgsinα,故B在C上下滑.
以C为研究对象,分析受力如图.

A、B对C的压力大小为 N1=N2=mgcosα,A对C的静摩擦力 f1=mgsinα,B对C的滑动摩擦力 f2=μ1mgcosα= ![]() mgsinα
mgsinα
因为(N1+N2)sinα=2mgcosαsinα,(f1+f2)cosα= ![]() mgcosαsinα,则C相对于地面有向左运动的趋势,地面对C的摩擦力水平向右,大小为 f=(N1+N2)sinα﹣(f1+f2)cosα=
mgcosαsinα,则C相对于地面有向左运动的趋势,地面对C的摩擦力水平向右,大小为 f=(N1+N2)sinα﹣(f1+f2)cosα= ![]() mgcosαsinα
mgcosαsinα
地面与C间的最大静摩擦力 fm=μ[Mg+(N1+N2)cosα+(f1+f2)sinα]
要使C依然能保持在地面不动,必须有 f≤fm,解得:
μ≥ ![]()
【解析】(1)物块能在C的斜面上保持静止,物块的重力沿斜面向下的分力不大于最大静摩擦力,由摩擦力公式列式求解.(2)A、B一起沿斜面体C的斜面匀速下滑,合力均为零,以整体为研究对象,由平衡条件和摩擦力公式结合求解.若将A、B对调位置,对C研究,由平衡条件和摩擦力公式结合解答.
【考点精析】利用滑动摩擦力和静摩擦力对题目进行判断即可得到答案,需要熟知滑动摩擦力:利用公式f=μF N 进行计算,其中FN 是物体的正压力,不一定等于物体的重力,甚至可能和重力无关.或者根据物体的运动状态,利用平衡条件或牛顿定律来求解;静摩擦力:静摩擦力大小可在0与fmax 之间变化,一般应根据物体的运动状态由平衡条件或牛顿定律来求解.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案