��Ŀ����
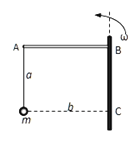
����Ŀ����ͼ��ʾ���ڶ�Ħ��������=0.2��ˮƽ������һ������Ϊm=2kg��С��С����ˮƽ�ᵯ�ɼ�����ֱ����ɦ�=45��ǵIJ����쳤������һ����������ʱС���ھ�ֹƽ��״̬����ˮƽ���С��ĵ���ǡ��Ϊ�㡣ȡg=10m/s2����С�������֮������Ħ������С���ڻ���Ħ�����Ĵ�С������������˲�䣬����˵��������ȷ����
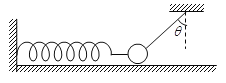
A. ��ʱ�ᵯ�ɵĵ�����СΪ20 N
B. ������������������20 N
C. С��ļ��ٶȴ�СΪ8 m/s2����������
D. �����ϵ��ɣ�����ϵ�˲��С��ļ��ٶȴ�СΪ10 m/s2
���𰸡�D
���������ȷ�����������ǰ���ɵĵ��������о���������˲�䣬ץס���ɵĵ���û�б仯�����С��ĺ�������ţ�ٵڶ��������С��ļ��ٶȺ�ˮƽ���С�������������������ǰ��С��������ͼ��ʾ
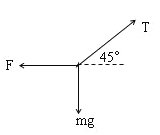
���ڴ��ھ�ֹ״̬�����ݹ�����ƽ�������ɵ�![]()
![]()
![]() ������ţ�ٵڶ����ɵã����ٶ�
������ţ�ٵڶ����ɵã����ٶ�![]() ������ˮƽ����C��ȷ�����ϵ��ɵ�˲�䣬������С�������˲��Ϊ�㣬��ʱС�����ܵĺ���Ϊ�㣬��С��ļ��ٶ�Ϊ�㣬��D����
������ˮƽ����C��ȷ�����ϵ��ɵ�˲�䣬������С�������˲��Ϊ�㣬��ʱС�����ܵĺ���Ϊ�㣬��С��ļ��ٶ�Ϊ�㣬��D����

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�