题目内容
 在实验室研究一辆质量为0.6kg的电动玩具车的运动情况,已知玩具车在头4s内由电动机牵引前进,后6s钟关闭了电动机.实验得到小车在10s内的运动图象v-t图如图所示:求
在实验室研究一辆质量为0.6kg的电动玩具车的运动情况,已知玩具车在头4s内由电动机牵引前进,后6s钟关闭了电动机.实验得到小车在10s内的运动图象v-t图如图所示:求(1)玩具车在滑行过程中所受阻力大小是多少?
(2)玩具车电动机产生的牵引力有多大?
(3)玩具车在全过程中的位移为多大?
分析:(1)根据加速度的定义公式求解减速过程的加速度,然后根据牛顿第二定律列式求解;
(2)先根据图象得到加速过程的加速度,然后根据牛顿第二定律列式求解;
(3)v-t图象与时间轴包围的面积表示位移.
(2)先根据图象得到加速过程的加速度,然后根据牛顿第二定律列式求解;
(3)v-t图象与时间轴包围的面积表示位移.
解答:解:(1)减速过程的加速度为:a=
=
=-
m/s2;
减速过程受重力、支持力和摩擦力,根据牛顿第二定律,有:-f=ma,解得:f=-ma=0.2N;
(2)加速过程的加速度为:a′=
=
=
m/s2;
加速过程受重力、支持力、牵引力和摩擦力,根据牛顿第二定律,有:F-f=ma′;
解得:F=ma′+f=0.6×
+0.2=0.5N;
(3)v-t图象与时间轴包围的面积表示位移,故
x=
×10×2=10m;
答:(1)玩具车在滑行过程中所受阻力大小是0.2N;
(2)玩具车电动机产生的牵引力有0.5N;
(3)玩具车在全过程中的位移为10m.
| △v |
| △t |
| -2 |
| 10-4 |
| 1 |
| 3 |
减速过程受重力、支持力和摩擦力,根据牛顿第二定律,有:-f=ma,解得:f=-ma=0.2N;
(2)加速过程的加速度为:a′=
| △v |
| △t |
| 2 |
| 4 |
| 1 |
| 2 |
加速过程受重力、支持力、牵引力和摩擦力,根据牛顿第二定律,有:F-f=ma′;
解得:F=ma′+f=0.6×
| 1 |
| 2 |
(3)v-t图象与时间轴包围的面积表示位移,故
x=
| 1 |
| 2 |
答:(1)玩具车在滑行过程中所受阻力大小是0.2N;
(2)玩具车电动机产生的牵引力有0.5N;
(3)玩具车在全过程中的位移为10m.
点评:本题关键根据图象得到运动情况,求解出加速度后,根据牛顿第二定律确定受力情况,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
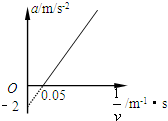 (2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为
(2011?河东区一模)(1)一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数(1/v)图象如图所示.若已知汽车的质量为m=1.5×103kg,则汽车运行时的功率为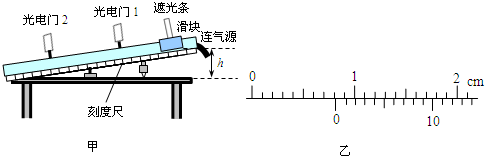
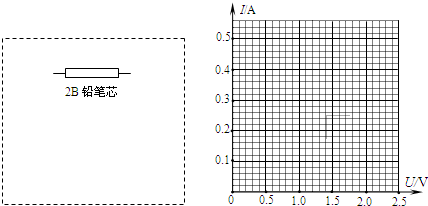
 在实验室研究一辆质量为0.6kg的电动玩具车的运动情况,已知玩具车在头4s内由电动机牵引前进,后6s钟关闭了电动机.实验得到小车在10s内的运动图象v-t图如图所示:求
在实验室研究一辆质量为0.6kg的电动玩具车的运动情况,已知玩具车在头4s内由电动机牵引前进,后6s钟关闭了电动机.实验得到小车在10s内的运动图象v-t图如图所示:求
