题目内容
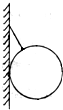如图所示，球的质量为m，用绳子挂在竖直的墙壁上处于平衡，绳长等于球的半径，球面光滑．试求球受到墙壁的弹力和绳子的拉力分别是多大？
解：设绳子与墙的夹角为β，则由几何知识得：β=30°．
对球受力分析如图，则由三力平衡条件可得：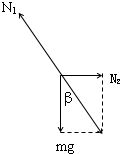
细线的拉力 N1=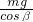
=
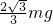
墙壁对球的弹力 N2=mgtanβ=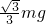
．
答：球受到墙壁的弹力和绳子的拉力分别是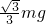和．
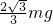分析：分析球的受力情况：重力mg、细绳的拉力N1和墙壁的弹力N2作用，作出球的受力示意图．根据平衡条件求解绳子对球的拉力大小及墙壁对球的弹力大小．
点评：物体处于共点力平衡时合力等于零，处理共点力平衡的方法有：合成法、正交分解法等．
对球受力分析如图，则由三力平衡条件可得：
细线的拉力 N1=
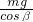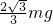
=墙壁对球的弹力 N2=mgtanβ=
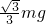．答：球受到墙壁的弹力和绳子的拉力分别是
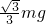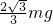和．分析：分析球的受力情况：重力mg、细绳的拉力N1和墙壁的弹力N2作用，作出球的受力示意图．根据平衡条件求解绳子对球的拉力大小及墙壁对球的弹力大小．
点评：物体处于共点力平衡时合力等于零，处理共点力平衡的方法有：合成法、正交分解法等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
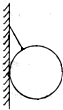如图所示，球的质量为m，用绳子挂在竖直的墙壁上处于平衡，绳长等于球的半径，球面光滑．试求球受到墙壁的弹力和绳子的拉力分别是多大？
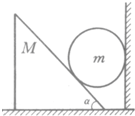如图所示，球的质量为m，斜面体的质量为M，斜面倾角为α，球与墙和斜面间均无摩擦，斜面体与地面间接触面粗糙，球与斜面体都处于静止状态，求地面对斜面体的支持力和摩擦力的大小．
