题目内容
在光滑水平面上有一静止的物体,现以水平恒力甲推这个物体,作用一段时间后,换成相反方向的水平恒力乙推这一物体,当恒力乙作用时间与恒力甲作用时间相同时,物体恰好回到原处,此时物体的动能为32J,则在整个过程中;
(1)恒力甲做的功为多少?
(2)恒力乙做的功为多少?
(1)恒力甲做的功为多少?
(2)恒力乙做的功为多少?
分析:物体先做匀加速运动,后做匀减速运动回到原处,整个过程中的位移为零.
根据牛顿第二定律和运动学公式即可确定两个力的大小关系,然后利用动能定理对全过程列式即可解.
根据牛顿第二定律和运动学公式即可确定两个力的大小关系,然后利用动能定理对全过程列式即可解.
解答:解:物体从静止起受水平恒力F甲 作用,做匀加速运动,经一段时间t后的速度为V1=a1t=
t,
以后受恒力F乙,做匀减速运动 a2=
,
经同样时间后回到原处,整个时间内在联系物体的位移为零,
于是
a1t2+V1t-
a2t2=0
解得 F乙=3F甲,
设在作用下物体的位移为L,对全过程用动能定理得:
F甲L+F乙L=△EK
即F甲L+3 F甲L=△EK
所以,恒力甲和乙做的功分别为,
W甲=F甲L=
△EK=8J
W乙=F乙L=
△EK=24J
答:(1)恒力甲做的功为8J;
(2)恒力乙做的功为24J.
| F甲 |
| m |
以后受恒力F乙,做匀减速运动 a2=
| F乙 |
| m |
经同样时间后回到原处,整个时间内在联系物体的位移为零,
于是
| 1 |
| 2 |
| 1 |
| 2 |
解得 F乙=3F甲,
设在作用下物体的位移为L,对全过程用动能定理得:
F甲L+F乙L=△EK
即F甲L+3 F甲L=△EK
所以,恒力甲和乙做的功分别为,
W甲=F甲L=
| 1 |
| 4 |
W乙=F乙L=
| 3 |
| 4 |
答:(1)恒力甲做的功为8J;
(2)恒力乙做的功为24J.
点评:在甲和乙的作用下,在相同的时间内,物体回到原处,说明位移的大小相同,这是解这道题的关键点,找到它们的关系,利用动能定理即可求得.

练习册系列答案
相关题目
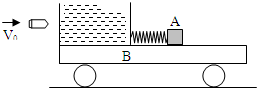 如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:
如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:

