题目内容
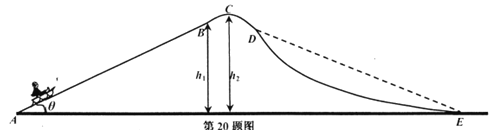
【题目】雪橇运动在北方很受人们欢迎，其简化模型如图所示。倾角θ=37°的直线雪道AB与曲线雪道BCDE在B点平滑连接，其中A、E两点在同一水平面上，雪道最高点C所对应的圆弧半径R=10m，B、C两点距离水平面AE的高度分别为h1=18m、h2=18.1m，雪橇与雪道间的动摩擦因数μ=0.1。游客可坐在电动雪橇上由A点从静止开始向上运动。若电动雪橇以恒定功率P=1.03kW工作t=10s时间后自动关闭，则雪橇和游客（总质量M=50kg）到达C点时的速度vC=1m/s，到达E点时的速度vE=9m/s。已知雪橇运动过程中不脱离雪道，sin37°=0.6，重力加速度g取10m/s2。
(1)求雪橇在C点时对雪道的压力；
(2)求雪橇在BC段克服摩擦力做的功；
(3)求雪橇从C点运动到E点过程中损失的机械能；
(4)若仅将DE段改成与曲线雪道CD段平滑连接的倾斜直线轨道（如图中虚线所示），则雪橇从C点运动到E点过程中损失的机械能将如何变化（增加，减少还是不变）？请简要说明理由。
【答案】（1）495N（2）25J（3）7050J（4）
不变
【解析】试题分析：选雪橇和游客的整体为研究对象，对其运动到C点进行受力分析，运用牛顿第二定律即可求出雪橇在C点时对雪道的压力；从A到C对雪橇和游客的整体运用动能定理，即可求出雪橇在BC段克服摩擦力做的功；对整体从C到E运用动能定理，求出摩擦力做功，根据功能原理即可求出C点运动到E点过程中损失的机械能；运用微积分思想求出曲线轨道上摩擦力做功，与倾斜直线轨道上摩擦力做功做比较，即可判断雪橇和游客的整体从C点运动到E点过程中损失机械能的情况。
（1）设C点轨道对雪橇的支持力为NC，根据牛顿第二定律可得： 
代入数据解得： 
根据牛顿第三定律可得，雪橇在C点时对雪道的压力：NC′=NC=495N
（2）设雪橇在BC段克服摩擦力做的功为WBC，从A到C对雪橇和游客的整体运用动能定理可得： 
代入数据解得：WBC=25J
（3）对整体从C到E运用动能定理可得： 
代入数据解得从C到E克服摩擦力做功：WCE=7050J
所以整体从C点运动到E点过程中损失的机械能：W损=WCE=7050J
（4）设D到E的水平距离为L，平滑连接的倾斜直线轨道倾角为θ，
摩擦力做功： 
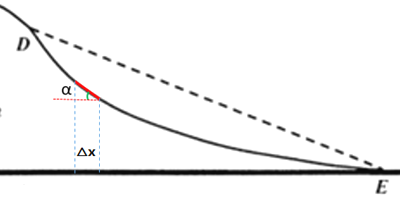
曲线轨道上任选极短一段如图所示，将这一小段近似看成倾角为α的倾斜直线轨道，该端轨道在水平方向上的投影长为△x，则摩擦力在该段轨道上做功： 
，所以整个曲线轨道摩擦力做功等于每一小段摩擦力做功的累加，即： 
故两轨道的摩擦力做功相同： 
所以雪橇和游客的整体从C点运动到E点过程中损失的机械能相同。
