题目内容
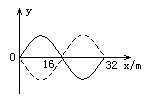
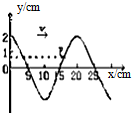
一列简谐波在x轴上传播,如图12-3-13,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示.已知Δt=t2-t1="0.1" s,问:
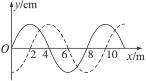
图12-3-13
(1)若波沿x轴正方向传播,且Δt<T,这列波的传播速度是多大?
(2)若波沿x轴正方向传播,但Δt无约束条件,波速是多大?
(3)若传播方向及周期均无约束条件,波速是多大?
(4)若波速v="340" m/s,则波向哪个方向传播?

图12-3-13
(1)若波沿x轴正方向传播,且Δt<T,这列波的传播速度是多大?
(2)若波沿x轴正方向传播,但Δt无约束条件,波速是多大?
(3)若传播方向及周期均无约束条件,波速是多大?
(4)若波速v="340" m/s,则波向哪个方向传播?
(1)v="20" m/s
(2)v="20(4n+1)" m/s(n=0,1,2,…)
(3)波沿x轴正方向传播,v="20(4n+1)" m/s(n=0,1,2,…)波沿x轴负方向传播,v="20(4n+3)" m/s(n=0,1,2,…)
(4)向x轴正方向传播.
(2)v="20(4n+1)" m/s(n=0,1,2,…)
(3)波沿x轴正方向传播,v="20(4n+1)" m/s(n=0,1,2,…)波沿x轴负方向传播,v="20(4n+3)" m/s(n=0,1,2,…)
(4)向x轴正方向传播.
(1)从图知,该波的波长为8 m,因Δt<T,故Δx<λ,由图知Δt=T/4,T="0.4" s,则:v="λ/T=20" m/s.
(2)由于Δt无约束条件,由振动的周期性,则Δt=(n+1/4)T,T=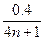 s,则:v=λ/T=20(4n+1) m/s.
s,则:v=λ/T=20(4n+1) m/s.
(3)因传播方向及周期均无约束条件,则波传播的双向性和时间周期性均要考虑:
当波沿x轴正方向传播,由振动的周期性,则Δt=(n+1/4)T,T=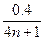 s,则:v=λ/T=20(4n+1) m/s.
s,则:v=λ/T=20(4n+1) m/s.
当波沿x轴负方向传播,由振动的周期性,则Δt=(n+3/4)T,T=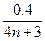 s,则:v=λ/T=20(4n+3) m/s.
s,则:v=λ/T=20(4n+3) m/s.
(4)波在Δt时间内移动的距离Δx="v·Δt=340×0.1" m/s="34" m/s=4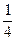 λ,由图可知向x轴正方向传播.
λ,由图可知向x轴正方向传播.
(2)由于Δt无约束条件,由振动的周期性,则Δt=(n+1/4)T,T=
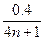 s,则:v=λ/T=20(4n+1) m/s.
s,则:v=λ/T=20(4n+1) m/s.(3)因传播方向及周期均无约束条件,则波传播的双向性和时间周期性均要考虑:
当波沿x轴正方向传播,由振动的周期性,则Δt=(n+1/4)T,T=
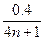 s,则:v=λ/T=20(4n+1) m/s.
s,则:v=λ/T=20(4n+1) m/s.当波沿x轴负方向传播,由振动的周期性,则Δt=(n+3/4)T,T=
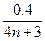 s,则:v=λ/T=20(4n+3) m/s.
s,则:v=λ/T=20(4n+3) m/s.(4)波在Δt时间内移动的距离Δx="v·Δt=340×0.1" m/s="34" m/s=4
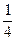 λ,由图可知向x轴正方向传播.
λ,由图可知向x轴正方向传播.
练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目