题目内容
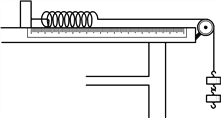
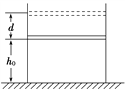
【题目】如图所示，在竖直放置的圆柱形容器内用质量为m的活塞密封一部分气体，活塞与容器壁间能无摩擦滑动，容器的横截面积为S，将整个装置放在大气压恒为p0的空气中，开始时气体的温度为T0，活塞与容器底的距离为h0，当气体从外界吸收热量Q后，活塞缓慢上升d后再次平衡，问：
(1)外界空气的温度是多少？
(2)在此过程中的密闭气体的内能增加了多少？
【答案】（1）
(2)Q－(mg＋p0S)d
【解析】试题分析：于封闭的气体，发生了等压变化，由盖吕萨克定律可求出外界空气的温度．活塞上升的过程，密闭气体克服大气压力和活塞的重力做功，根据势力学第一定律求得气体的内能增加量。
（1）取密闭气体为研究对象，活塞上升过程为等压变化，
由盖·吕萨克定律有
解得外界温度： 
(2)活塞上升的过程，密闭气体克服大气压力和活塞的重力做功，
所以外界对系统做的功：W＝－(mg＋p0S)d，
根据热力学第一定律得密闭气体增加的内能ΔU＝Q＋W＝Q－(mg＋p0S)d.
练习册系列答案
灵星计算小达人系列答案
相关题目
【题目】若测得某一物体质量m一定时，a与F的有关数据资料如表所示：
a/ms﹣2 | 1.98 | 4.06 | 5.95 | 8.12 |
F/N | 1.00 | 2.00 | 3.00 | 4.00 |
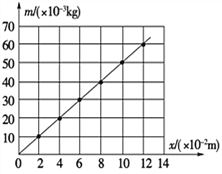
（1）根据表中数据，画出a﹣F图象________（图1）．
（2）根据图象判定：当m一定时，a与F的关系为_______．
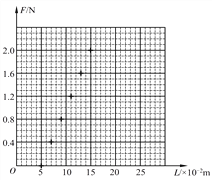
（3）若甲、乙两同学在实验过程中，由于没有按照正确步骤进行实验，处理数据后得出如图2所示的a﹣F图象．试分析甲、乙两同学可能存在的问题：甲：_______；乙：_______．
