��Ŀ����
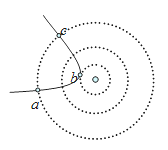
����Ŀ����ͼ��ʾΪ��ɽ������ģ�ͣ����ɹ⻬ˮƽ�������ֱ���ڵĹ⻬Բ�ι����ɣ�Q��ΪԲ�ι����͵㣬M��Ϊ��ߵ㣬Բ�ι���뾶R��0.32m.ˮƽ���PN�Ҳ��ˮƽ�����ϣ����ŷ������鳤ľ��c��d����ľ�����Ӵ�����ճ������ľ���ϱ�����ˮƽ���PNƽ�룬ľ��c����m3��2.2kg����L��4m��ľ��d����m4��4.4kg.����m2��3.3kg��С����b�����ڹ��QN�ϣ���һ����m1��1.3kg��С����a��P����ˮƽ�ٶ�v0�����˶�����Բ�ι���˶�һ�ܺ����ˮƽ�����С����b������ײ����ײʱ�伫������ײ��������е����ʧ.����a��ԭ·���ص�M��ʱ���Թ��ѹ��ǡ��Ϊ0.��֪С����b�����鳤ľ��䶯Ħ��������Ϊ��0��0.16���������ٶ�g��10m/s2.
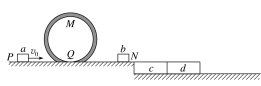
(1)��С����a��С����b��ײ��a��b���ٶȴ�Сv1��v2��
(2)������b��ľ��c��d�ϻ���ʱ��ľ��c��d����ֹ������c��d������Ķ�Ħ�����������ٶ��(ľ��c��d������Ķ�Ħ��������ͬ�����Ħ�������ڻ���Ħ����)
(3)������ľ��c��d�������Ħ��������b����ǡ��û���뿪ľ��d����b��ľ��c�ϻ��е�ʱ�估ľ��d�ij���.
���𰸡�(1)4m/s 5.2 m/s (2)0.069 (3)1s 1.4m
��������(1)���������֪��С����a���ص�M��ʱ��
m1![]() ��m1g
��m1g
С����a���ص�M������л�е���غ㣺
![]() m1v
m1v![]() ��
��![]() m1v
m1v![]() ��m1g(2R)
��m1g(2R)
�������ݣ���ã�v1��4m/s
ȡˮƽ����Ϊ������С����a��b��ײǰ��
�����غ㣺m1v0����m1v1��m2v2
��е���غ㣺![]() m1v
m1v![]() ��
��![]() m1v
m1v![]() ��
��![]() m2v
m2v![]()
�������ݣ���ã�v0��9.2m/s��v2��5.2 m/s
(2)��b��d�ϻ���ʱd�ܾ�ֹ����b��c�ϻ���ʱc��dһ���ܾ�ֹ
��(m2��m4)g>��0m2g
��æ�>![]() ��0��0.069
��0��0.069
(3)С����b���ϳ�ľ��cʱ�ļ��ٶȴ�С��
a1����0g��1.6m/s2
��ʱ���鳤ľ��ļ��ٶȴ�С��a2��![]() g��0.8m/s2
g��0.8m/s2
��С����b�ڳ�ľ��c�ϵĻ���ʱ��Ϊt����
ʱ��t��С����b��λ��x1��v2t��![]() a1t2
a1t2
���鳤ľ���λ��x2��![]() a2t2
a2t2
��x1��x2��L
��ã�t1��1s��t2��![]() s(��ȥ)
s(��ȥ)
b���뿪��ľ��cʱb���ٶ�v2�䣽v2��a1t1��3.6m/s
b���뿪��ľ��cʱd���ٶ�v3��a2t1��0.8m/s
d�ij�������Ϊx��
�ɶ����غ��֪��m2v2�䣫m4v3��(m2��m4)v
��ã�v��2m/s
��0m2gx��![]() m2v2��2��
m2v2��2��![]() m4v
m4v![]() ��
��![]() (m2��m4)v2
(m2��m4)v2
��ã�x��1.4m