��Ŀ����
18���ڡ�̽�����������붯�ܸı��Ĺ�ϵ��ʵ���У�����ͼ1ʾװ�õ�ʵ�鷽����ʵ��ʱ��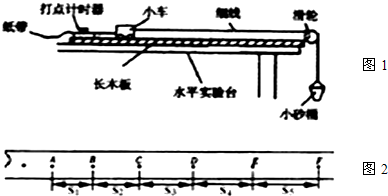
��1������ɰ��СͰ����������ʾС���ܵ��ĺ�����Ϊ�˼�����������������ʵ�������룺��ʹ��ľ�����̧��-�����ʵĽǶȣ���ƽ��Ħ������������������С������Զ����ɰ��СͰ����������ѡ�Զ���ڡ�����ԶС�ڡ��������ڡ�������ʹ����С����ϸ�ߣ�С��-���ֶΣ��볤ľ��ƽ�У�
��2����ͼ2��ʾ��ij��ʵ���еõ���һ��ֽ��������A��B��C��D��E��F�Ǽ����㣬���ڼ�������ʱ����ΪT��������ͼ��ʾ�����C��ʱС�����ٶ�vc����ʽΪ��������������������ʾ��${v}_{C}=\frac{{s}_{2}+{s}_{3}}{2T}$��Ҫ��֤�����������붯�ܱ仯��Ĺ�ϵ������Ҫ����ɰ��СɰͰ��������������С����λ�ơ��ٶ��⣬��Ҫ�������������С����������
���� 1��С����ˮƽ������������������Ħ���������ù����������ʾС���ܵ��ĺ�������������Ҫƽ��Ħ���������Ҫ���ù����������ʾС���ܵ��ĺ�����������Ҫ���㹳�������ԶС��С������������
2��Ϊ��ʹ��ɳ��ɳͰ����������ʾС���ܵ��ĺ�����������ȡ��ʩ����֤ţ�ٵڶ��������ƣ����ݶ��ܶ����ı���ʽ��������ȷ������������
��� �⣺��1������ɰ��СͰ����������ʾС���ܵ��ĺ�����Ϊ�˼�����������������ʵ�������룺
��ʹ��ľ�����̧��-�����ʵĽǶȣ���ƽ��Ħ�������Ա�֤�������������ӵ�������
������������С������ Զ����ɰ��СͰ�����������Ա�֤���ӵ���������ɳ��СͰ����������
��ʹ����С����ϸ�ߣ�С��---���ֶΣ��볤ľ��ƽ�У��Ա�֤�������������ӵ�������
��2�������ȱ���ֱ���˶����ص㣬C����ٶȵ���BD֮���ƽ���ٶȣ����ԣ�${v}_{C}=\frac{{s}_{2}+{s}_{3}}{2T}$
ƽ��Ħ������С���ܵ��ĺ���Ϊmg���������Ĺ����ڶ��ܵı仯�������Ҫ��֤�ı���ʽΪ��mgs=$\frac{1}{2}$mvB2-$\frac{1}{2}$mvA2��
�ʻ���Ҫ�������������С����������
�ʴ�Ϊ����1��ƽ��Ħ���� ��Զ���� ��ƽ��
��2��${v}_{C}=\frac{{s}_{2}+{s}_{3}}{2T}$��������
���� ��̽�����������붯�ܸı�Ĺ�ϵ���롰̽�����ٶ������������Ĺ�ϵ���кܶ�����֮������ƽʱѧϰ��Ҫ�����ܽᡢ�Ƚϣ���߶�ʵ�������������

| A�� | �ٶ���С�ı�����˶� | B�� | �ٶ�������ı�����˶� | ||
| C�� | ����СΪ��ʱ���ٶ�Ҳ��СΪ�� | D�� | ����СΪ��ʱ���ٶȴﵽ���ֵ |
| A�� | F=8 N | B�� | F=9 N | C�� | f=3 N | D�� | f=6 N |
| A�� | ���ٶȴ�Сһ���ı� | B�� | ���ٶȴ�Сһ���ı� | ||
| C�� | �ٶȷ���һ���ı� | D�� | ��������Сһ���ı� |
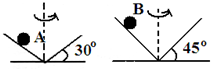 ��ͼ��ʾ�����⻬Բ����ˮƽ��ļнǷֱ�Ϊ30���45�㣬������ͬС��ֱ�����Բ���ڲ�����������Բ���˶�����С����Ϊ�ʵ��ҽ��ٶ���ͬ���������ٶ�Ϊg��������
��ͼ��ʾ�����⻬Բ����ˮƽ��ļнǷֱ�Ϊ30���45�㣬������ͬС��ֱ�����Բ���ڲ�����������Բ���˶�����С����Ϊ�ʵ��ҽ��ٶ���ͬ���������ٶ�Ϊg��������| A�� | �������������С֮�ȣ�${F_A}��{F_B}=\sqrt{3}��3$ | |
| B�� | ��������ٶȴ�С֮�ȣ�${v_A}��{v_B}=3��\sqrt{3}$ | |
| C�� | ��������֧������С֮�ȣ�${N_A}��{N_B}=\sqrt{2}��\sqrt{3}$ | |
| D�� | ��������ļ��ٶȴ�С��С֮��Ϊ��${a_A}��{a_B}=3��\sqrt{3}$ |
| A�� | $\frac{5F}{64}$ | B�� | 0 | C�� | $\frac{3F}{64}$ | D�� | $\frac{3F}{16}$ |
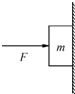
| A�� | ��Ϊľ�龲ֹ����֪F=mg | |
| B�� | ľ���ܵ���Ħ�����ķ���������� | |
| C�� | ���F����ľ����ǽ�ڼ�ľ�Ħ����Ҳ���� | |
| D�� | ���F����ľ����ǽ�ڼ��Ħ�����Բ��� |
 ��ͼ��ʾ��һ������m=60kg�����壬��v0=2m/s�ij��ٶ���ɽ���ȼ��ٻ��£�ɽ�µ���Ǧ�=30�㣬��t=4s��ʱ���ڻ��µľ���Ϊ40m���������ܵ�������������������Ħ�����Ϳ���������
��ͼ��ʾ��һ������m=60kg�����壬��v0=2m/s�ij��ٶ���ɽ���ȼ��ٻ��£�ɽ�µ���Ǧ�=30�㣬��t=4s��ʱ���ڻ��µľ���Ϊ40m���������ܵ�������������������Ħ�����Ϳ���������