题目内容
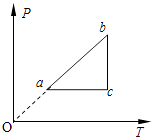
【题目】小球从空中自由下落，与水平地面第一次相碰后反弹到空中某一高度，其速度随时间变化的关系如图所示．若g=10m/s2，则（ ）
A. 小球第一次反弹后离开地面的速度的大小为5m/s
B. 碰撞前后速度改变量的大小为8m/s
C. 小球是从5m高处自由下落的
D. 小球反弹起的最大高度为0.45m
【答案】BD
【解析】由图象可知：0.5s末物体反弹，此时速度的大小为3m/s，故A错误；碰撞时速度的改变量为△v=-3m/s-5m/s=-8m/s，则速度的改变量大小为8m/s，故B正确；由图象可知：前0.5s内物体自由下落，后0.3s物体反弹，根据v-t图象中速度图象与时间轴围成的面积表示位移可得：小球下落的高度为：h=
×0.5×5m=1.25m．故C错误；小球能弹起的最大高度对应图中0.6s-0.8s内速度图象的面积，所以h=×0.3×3m=0.45m，故D正确；故选BD.
【题目】在做“研究匀变速直线运动”的实验中：
（1）实验室提供了以下器材：打点计时器、一端附有滑轮的长木板、小车、纸带、细绳、钩码、刻度尺、导线、交流电源、复写纸、弹簧测力计．其中在本实验中不需要的器材是 ．
（2）根据打点计时器打出的纸带，我们可以直接得到的物理量是
A.瞬时速度
B.加速度
C.时间间隔
D.平均速度
（3）如图1所示是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，打点计时器打点的时间间隔T=0.02s，其中x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.26cm．
下表列出了打点计时器打下B、C、F时小车的瞬时速度，请在表中填入打点计时器打下D、E两点时小车的瞬时速度
位置 | B | C | D | E | F |
速度/（ms﹣1） | 0.737 | 0.801 | 0.994 |
（4）以A点为计时起点，在坐标图2中画出小车的速度﹣时间关系线．
（5）根据你画出的小车的速度﹣时间关系图线计算出小车的加速度a=m/s2 ．
【题目】某物理兴趣小组利用传感器进行探究实验，其实验装置及原理图分别如甲、乙所示．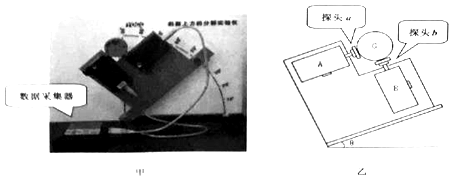
该装置中，A、B为力传感器，研究对象是质量m=310g的金属圆柱体G，将G放在A、B的两探头之间，两探头受到压力的数据，通过传感器、数据采集器传输给计算机，数据如表1所示．
表1 圆柱体的质量：310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.49 | 2.12 | 2.59 | 3.02 |
FB/N | 3.01 | 2.61 | 2.13 | 1.50 | 0.00 |
（1）观察、分析数据表1，可得出：金属圆柱体重力沿斜面向下的分力FA随斜面倾角θ的增大而 ， 垂直斜面向下的分力FB随斜面倾角θ的增大而 ．
（2）某同学发现两传感器的读数并不是与角度的变化成正比，他猜想圆柱体所受重力及其分力间满足某个函数关系，并根据该函数关系计算两探头受到压力的理论值如表2所示（g取9.8m/s2）
表2 圆柱体的质量：310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.52 | 2.15 | 2.63 | 3.04 |
FB/N | 3.04 | 2.63 | 2.15 | 1.52 | 0.00 |
该同学猜测的函数关系式应当分别为：FA= ， FB=（用金属圆柱体质量m、重力加速度g、斜面倾角θ表示）
（3）在实验中无论是分析“表1”还是“表2”的数据时，都认为传感器的读数都等于相应的圆柱体重力的分力，其物理学依据是（乙沿斜面方向为例）；因为A传感器的读数等于A传感器所受的压力，根据此压力大小等于圆柱体沿斜面方向所受的支持力，而根据此支持力大小等于圆柱体重力沿斜面方向的分力
（4）为了减少实验误差，可采取的办法是（写出一个即可）
