Question

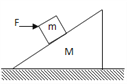
【题目】某同学设想用带电粒子的运动轨迹做出“0”、“8”字样，首先，如图甲所示，在真空空间的竖直平面内建立xOy坐标系，在y1=0.1m和y2=-0.lm处有两个与x轴平行的水平界面PQ和MN把空间分成Ⅰ、Ⅱ、Ⅲ三个区域，在三个区域中分别存在匀强磁场B1、B2、B3，其大小满足B2= 2B1= 2B3=0.02T,方向如图甲所示。在Ⅱ区域中的y轴左右两侧还分別存在匀强电场E1、E2(图中未画出）。忽格所有电、磁场的边缘效应，ABCD基以坐标原点O为中心对称的正方形，其边长L=0.2m。现在界面PQ上的A处沿y轴正方向发射一比荷的带正电荷的粒子（其重力不计），粒子恰能沿图中实线途经BCD三点后回到A点并做周期性运动，轨迹构成一个“0”字。已知粒子每次穿越II区域时均做直线运动。

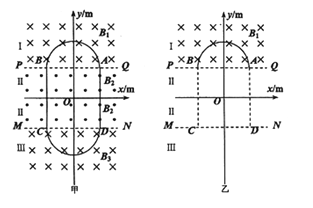
(1)E1、E2的大小和方向；

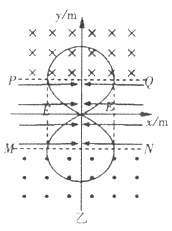
(2)去掉II和Ⅲ区域中的匀强电场和磁场，其他条件不变，仍在A处以相同的速度发射相同的粒子，请在Ⅱ和Ⅲ区城内重新设计适当的匀强电场或匀强磁场，使粒子运动的轨迹成为上、下对称的“8”字，且粒子运动的周期跟甲图中相同，请通过必要的计算和分析，求出你所设计的“场”的大小、方向和区域, 并在乙图中描给出带电粒子的运动轨迹和你所设计的“场”。（上面半圆轨迹N在图中画出）

Answer 1

【答案】（1）方向水平向右，方向水平向左；

（2）如图所示：

【解析】(1)在I、Ill区域中

解得

在Ⅱ区域的电磁场中运动满足B2qv=qE1

解得E1=B2v=0.02×105=2×103V/m，方向水平向右

同理,E2=v0B2=2×103N/C，方向水平向左

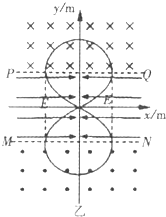
(2)根据对称性，在区域Ⅲ中只能存在匀强磁场，满足B3=B1=0.01T，方向垂直纸面向外，由于周期相等，所以在区域Ⅱ中只能存在匀强电场，且方向必须与x轴平行。从B点运动至O点做类平抛运动，时间t=y1/v=106s

沿x轴方向的位移为，则

由牛顿第二定律得：qE=ma

解得：E=2×103V/m

根据对称性，电场方向如图中Ⅱ区域箭头所示，运动轨迹如图所示.