题目内容
4. 如图所示,为测试子弹的发射速度,让子弹水平射向绕水平轴旋转的圆纸筒,纸筒的直径为d,角速度为ω,子弹沿直径水平穿过纸筒,只留下一个弹孔,则子弹的速度可能为$\frac{dω}{(2n-1)π}$,n=1、2、3….
如图所示,为测试子弹的发射速度,让子弹水平射向绕水平轴旋转的圆纸筒,纸筒的直径为d,角速度为ω,子弹沿直径水平穿过纸筒,只留下一个弹孔,则子弹的速度可能为$\frac{dω}{(2n-1)π}$,n=1、2、3….
分析 子弹沿圆筒直径穿过圆筒,结果发现圆筒上只有一个弹孔,在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,结合角速度求出时间,从而得出子弹的速度.
解答 解:在子弹飞行的时间内,圆筒转动的角度为(2n-1)π,n=1、2、3…,
则时间t=$\frac{(2n-1)π}{ω}$,
所以子弹的速度v=$\frac{d}{t}=\frac{dω}{(2n-1)π}$,n=1、2、3…,
故答案为:$\frac{dω}{(2n-1)π}$,n=1、2、3…
点评 解决本题的关键知道圆筒转动的周期性,结合转过角度的通项式得出运动的时间,抓住子弹飞行的时间和圆筒转动时间相等进行求解.

练习册系列答案
相关题目
19.一艘小船在静水中的速度为3m/s,渡过一条宽150m,水流速度为4m/s的河,则该小船( )
| A. | 最短渡河时间为30s | |
| B. | 最短渡河时间为50s | |
| C. | 调整船头方向,船可以到达正对岸 | |
| D. | 无论如何调整船头方向,船不可能到达正对岸 |
9. 向心力大小可能与物体的质量、圆周运动的半径,线速度、角速度有关,如图所示,用向心力演示器探究小球受到的向心力大小与角速度的关系时,下列做法可行的是 ( )
向心力大小可能与物体的质量、圆周运动的半径,线速度、角速度有关,如图所示,用向心力演示器探究小球受到的向心力大小与角速度的关系时,下列做法可行的是 ( )
 向心力大小可能与物体的质量、圆周运动的半径,线速度、角速度有关,如图所示,用向心力演示器探究小球受到的向心力大小与角速度的关系时,下列做法可行的是 ( )
向心力大小可能与物体的质量、圆周运动的半径,线速度、角速度有关,如图所示,用向心力演示器探究小球受到的向心力大小与角速度的关系时,下列做法可行的是 ( )| A. | 在小球运动半径不等的情况下,用质量不同的钢球做实验 | |
| B. | 在小球运动半径相等的情况下,用质量相同的钢球做实验 | |
| C. | 在小球运动半径不等的情况下,用质量相同的钢球做实验 | |
| D. | 在小球运动半径相等的情况下,用质量不同的钢球做实验 |
16.关于曲线运动,下列说法中正确的是( )
| A. | 物体做曲线运动时,它的速度可能保持不变 | |
| B. | 物体只有受到一个方向不断改变的力的作用,才可能做曲线运动 | |
| C. | 所有做曲线运动的物体,加速度方向与所受合外力方向不一致 | |
| D. | 所有做曲线运动的物体,所受合外力方向与速度方向肯定不在一条直线上 |
13.2009年2月11日,俄罗斯的“宇宙•2251”卫星和美国的“铱•33”卫星在西伯利亚上空约805km处发生碰撞,这是历史上首次发生的完整在轨卫星碰撞事件.碰撞过程中产生的大量碎片可能会影响太空环境.假定有甲、乙两块碎片,绕地球运动的轨道都是圆,甲的运行速率比乙的大,则下列说法中正确的是( )
| A. | 甲的运行周期一定比乙的长 | B. | 甲距地面的高度一定比乙的低 | ||
| C. | 甲的向心力一定比乙的大 | D. | 甲的加速度一定比乙的小 |
14. 如图,在今年5月下旬中俄联合军演中,歼-20战机在南海上空结队翱翔.飞行的某段时间内飞机在高空沿一水平面内的圆弧匀速盘旋,已知飞机质量为m(忽略该段时内耗油质量),速度大小为v,圆弧的半径为R,则( )
如图,在今年5月下旬中俄联合军演中,歼-20战机在南海上空结队翱翔.飞行的某段时间内飞机在高空沿一水平面内的圆弧匀速盘旋,已知飞机质量为m(忽略该段时内耗油质量),速度大小为v,圆弧的半径为R,则( )
 如图,在今年5月下旬中俄联合军演中,歼-20战机在南海上空结队翱翔.飞行的某段时间内飞机在高空沿一水平面内的圆弧匀速盘旋,已知飞机质量为m(忽略该段时内耗油质量),速度大小为v,圆弧的半径为R,则( )
如图,在今年5月下旬中俄联合军演中,歼-20战机在南海上空结队翱翔.飞行的某段时间内飞机在高空沿一水平面内的圆弧匀速盘旋,已知飞机质量为m(忽略该段时内耗油质量),速度大小为v,圆弧的半径为R,则( )| A. | 空气对飞机的作用力大小为m$\frac{{v}^{2}}{R}$ | |
| B. | 空气对飞机作用力大小为m$\sqrt{{g}^{2}+(\frac{{v}^{2}}{R})^{2}}$ | |
| C. | 空气对飞机竖直方向作用力大小为mg | |
| D. | 飞机的机械能保持不变 |
 浙江卫视六频道《我老爸最棒》栏目中有一项人体飞镖项目,可将该运动简化为以下模型(如图所示):手握飞镖的小孩用不可伸长的细绳系于天花板下,在A处被其父亲沿垂直细绳方向推出,摆至最低处B时松手,飞镖依靠惯性飞出命中竖直放置的圆形靶的靶心O,圆形靶的最高点C与B在同一高度,A、B、C三处在同一竖直平面内,且BC与圆形靶平面垂直.已知小孩质量为m,绳长为L,BC距离为s,靶的半径为R,AB高度差为h.不计空气阻力,小孩和飞镖均可视为原点.
浙江卫视六频道《我老爸最棒》栏目中有一项人体飞镖项目,可将该运动简化为以下模型(如图所示):手握飞镖的小孩用不可伸长的细绳系于天花板下,在A处被其父亲沿垂直细绳方向推出,摆至最低处B时松手,飞镖依靠惯性飞出命中竖直放置的圆形靶的靶心O,圆形靶的最高点C与B在同一高度,A、B、C三处在同一竖直平面内,且BC与圆形靶平面垂直.已知小孩质量为m,绳长为L,BC距离为s,靶的半径为R,AB高度差为h.不计空气阻力,小孩和飞镖均可视为原点.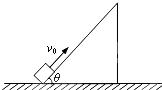 斜面固定在水平地面上,倾角θ=53°,斜面足够长,物体与斜面间的动摩擦因数μ=0.8,如图所示.一物体以v0=6.4m/s的初速度从斜面底端向上滑行,sin53°=0.8,cos53°=0.6,g取10m/s2,求
斜面固定在水平地面上,倾角θ=53°,斜面足够长,物体与斜面间的动摩擦因数μ=0.8,如图所示.一物体以v0=6.4m/s的初速度从斜面底端向上滑行,sin53°=0.8,cos53°=0.6,g取10m/s2,求