题目内容
【题目】如图所示,传送带A、B两点之间的距离L=3.2 m,与水平面夹角θ=37°,传送带沿顺时针方向转动,速度恒为v=2 m/s,在上端A点无初速度地放置一质量m=l kg、可视为质点的金属块,它与传送带间的动摩擦因数μ=0.5,金属块滑离传送带后,经过光滑弯道BC和光滑轨道CD,然后沿半径R=0.5 m的光滑半圆轨道DE做圆周运动,恰好能通过半圆轨道的最高点E,取sin 37°=0.6,cos 37°=0.8,重力加速度g=10 m/s2,则下列说法正确的是
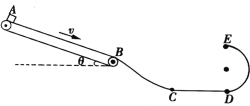
A.金属块在传送带上运动的时间为1.2 s
B.传送带对金属块所做的功为–16 J
C.金属块运动到D点的速度为0.5 m/s
D.B点和D点的高度差为0.45 m
【答案】AD
【解析】金属块刚放上传送带时有mgsin θ+μmgcos θ=ma1,解得a1=10 m/s2,设金属块经位移s1与传送带达到共同速度,由v2=2a1s1,解得s1=0.2 m<3.2 m,此过程所用时间t1=![]() =0.2 s,继续运动过程中有mgsin θ–μmgcos θ=ma2,解得a2=2 m/s2,由s2=L–s1=3 m,vB2–v2=2a2s2,解得vB=4 m/s,此过程所用时间时间t2=
=0.2 s,继续运动过程中有mgsin θ–μmgcos θ=ma2,解得a2=2 m/s2,由s2=L–s1=3 m,vB2–v2=2a2s2,解得vB=4 m/s,此过程所用时间时间t2=![]() =1 s,金属块在传送带上运动的时间t=t1+t2=1.2 s,A正确;金属块在传送带上运动的过程中,由动能定理有mgLsin θ+W=
=1 s,金属块在传送带上运动的时间t=t1+t2=1.2 s,A正确;金属块在传送带上运动的过程中,由动能定理有mgLsin θ+W=![]() mvB2–0,解得W=–11.2 J,即传送带对金属块所做的功为–11.2 J,B错误;由题意,金属块在E点时有mg=m
mvB2–0,解得W=–11.2 J,即传送带对金属块所做的功为–11.2 J,B错误;由题意,金属块在E点时有mg=m![]() ,金属块从D点到E点的过程中由动能定理有–2mgR=
,金属块从D点到E点的过程中由动能定理有–2mgR=![]() mvE2–
mvE2–![]() mvD2,解得vD=5 m/s,C错误;金属块从B点到D点过程,由动能定理有mgh=
mvD2,解得vD=5 m/s,C错误;金属块从B点到D点过程,由动能定理有mgh=![]() mvD2–
mvD2–![]() mvB2,解得h=0.45 m,D正确。
mvB2,解得h=0.45 m,D正确。

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】如图所示是用光电门传感器测定小车瞬时速度的情景,轨道上a、c间距离恰等于小车长度,b是a、c中点。某同学采用不同的挡光片做了三次实验,并对测量精确度加以比较。挡光片安装在小车中点处,光电门安装在c点,它测量的是小车前端P抵达_______(选填“a”“b”或“c”)点时的瞬时速度;若每次小车从相同位置释放,记录数据如表格所示,那么测得瞬时速度较精确的值为_______m/s。
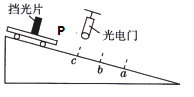
次序 | 挡光片宽/m | 挡光时间/s | 速度/(ms-1) |
1 | 0.080 | 0.036 | 2.22 |
2 | 0.040 | 0.020 | 2.00 |
3 | 0.020 | 0.0105 | 1.90 |