题目内容
如图所示,竖直面内一组合轨道由三部分组成;AB段为半径R=0.9m的半圆形,BC段水平、CD段为倾角为 =45°的足够长的斜面,各部分间均平滑连接。一质量为m=0.2kg(可视为质点)的小物块,从CD段上的某点M(M距BC的高度为h)由静止释放,小物块运动中与CD段动摩擦因数为μ=0.1,AB、BC部分光滑。取g=10m/s2,求
=45°的足够长的斜面,各部分间均平滑连接。一质量为m=0.2kg(可视为质点)的小物块,从CD段上的某点M(M距BC的高度为h)由静止释放,小物块运动中与CD段动摩擦因数为μ=0.1,AB、BC部分光滑。取g=10m/s2,求

小题1:若h=2m,小物块经圆轨道的最低点B时对轨道的压力;
小题2:h为何值时小物块才能通过圆轨道的最高点A?
 =45°的足够长的斜面,各部分间均平滑连接。一质量为m=0.2kg(可视为质点)的小物块,从CD段上的某点M(M距BC的高度为h)由静止释放,小物块运动中与CD段动摩擦因数为μ=0.1,AB、BC部分光滑。取g=10m/s2,求
=45°的足够长的斜面,各部分间均平滑连接。一质量为m=0.2kg(可视为质点)的小物块,从CD段上的某点M(M距BC的高度为h)由静止释放,小物块运动中与CD段动摩擦因数为μ=0.1,AB、BC部分光滑。取g=10m/s2,求
小题1:若h=2m,小物块经圆轨道的最低点B时对轨道的压力;
小题2:h为何值时小物块才能通过圆轨道的最高点A?
小题1:压力大小为10N,方向竖直向下
小题2:
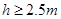
(1)小物块由M到B的过程,根据动能定理得
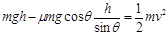 (2分)
(2分)
在B点,由牛顿第二定律得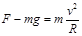 (2分)
(2分)
解得F="10N " (1分)
根据牛顿第三定律知:小物块在B点对轨道的压力大小为10N,方向竖直向下(1分)
(1)小物块通过最高点时,由牛顿第二定律得
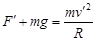 (1分)
(1分)
需满足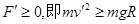
小物块由M到A的过程,由动能定理得
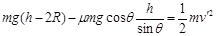 (1分)
(1分)
解得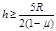
代入数据得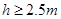 (2分)
(2分)
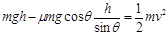 (2分)
(2分)在B点,由牛顿第二定律得
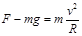 (2分)
(2分)解得F="10N " (1分)
根据牛顿第三定律知:小物块在B点对轨道的压力大小为10N,方向竖直向下(1分)
(1)小物块通过最高点时,由牛顿第二定律得
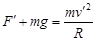 (1分)
(1分)需满足
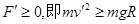
小物块由M到A的过程,由动能定理得
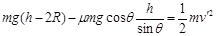 (1分)
(1分)解得
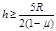
代入数据得
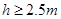 (2分)
(2分)
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目





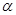 =53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
=53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求: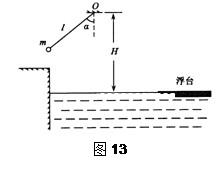
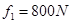 ,平均阻力
,平均阻力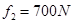 ,求选手落入水中的深度
,求选手落入水中的深度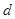 ;
;