题目内容
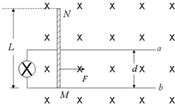 (2013?广东模拟)如图所示,水平放置的两条光滑平行金属导轨ab,相距为d=1m,导轨之间垂直放置一质量为m=1kg,长度L=2m的均匀金属棒MN,棒与导轨始终良好接触.棒的电阻r=2Ω,导轨的电阻忽略不计.左端导轨之间接有一电阻为R=2Ω的灯泡,整个装置放在磁感应强度B=2T的匀强磁场中,磁场方向垂直导轨平面向下.现对棒MN施加一水平向右的拉力F,使棒从静止开始运动,试求:
(2013?广东模拟)如图所示,水平放置的两条光滑平行金属导轨ab,相距为d=1m,导轨之间垂直放置一质量为m=1kg,长度L=2m的均匀金属棒MN,棒与导轨始终良好接触.棒的电阻r=2Ω,导轨的电阻忽略不计.左端导轨之间接有一电阻为R=2Ω的灯泡,整个装置放在磁感应强度B=2T的匀强磁场中,磁场方向垂直导轨平面向下.现对棒MN施加一水平向右的拉力F,使棒从静止开始运动,试求:(1)若施加的水平恒力F=8N,则金属棒达到的稳定速度为多少?
(2)在(1)的前提下,金属棒MN两端的电势差UMN
(3)若施加的水平外力功率恒为P=20W,经历t=1s时间,棒的速度达到2m/s,则此过程中灯泡产生的热量是多少?
分析:(1)金属棒在拉力作用下,做加速度逐渐减小的加速运动,当加速度为零时,速度达到最大,然后做匀速直线运动,根据金属棒所受的拉力等于安培力,求出最大速度;
(2)金属棒MN两端的电势差UMN分为两部分,连入闭合回路的一部分和未连入两部分,所以电势差UMN等于电路的路端电压和未连入电路两端电压值和;
(3)根据动能定理可求得该过程金属棒克服安培力做的功,根据功能关系即可求电路中产生的热能,然后根据串联电路中热量分配关系即可求解,
(2)金属棒MN两端的电势差UMN分为两部分,连入闭合回路的一部分和未连入两部分,所以电势差UMN等于电路的路端电压和未连入电路两端电压值和;
(3)根据动能定理可求得该过程金属棒克服安培力做的功,根据功能关系即可求电路中产生的热能,然后根据串联电路中热量分配关系即可求解,
解答:解:(1)稳定时金属棒平衡,设速度为v,
由平衡得:F=BId ①
由法拉第电磁感应定律 E=Bdv ②
由闭合电路欧姆定律得:I=
③
联立①②③得 v=6m/s ④
(2)UMN=U灯+B(L-d)v ⑤
由欧姆定律得:U灯=
R ⑥
联立②④⑤⑥得 UMN=20V ⑦
(3)设金属棒克服安培力做功为W,由动能定理得 Pt-W=
mv′2 ⑧
克服安培力做功转化为总电能,设为Q,则有Q=W ⑨
故灯泡发热为Q1=
Q ⑩
联立⑧⑨⑩得:Q1=12J
答:(1)若施加的水平恒力F=8N,则金属棒达到的稳定速度为6m/s;
(2)在(1)的前提下,金属棒MN两端的电势差UMN为20V;
(3)灯泡产生的热量是12J.
由平衡得:F=BId ①
由法拉第电磁感应定律 E=Bdv ②
由闭合电路欧姆定律得:I=
| E | ||
R+
|
联立①②③得 v=6m/s ④
(2)UMN=U灯+B(L-d)v ⑤
由欧姆定律得:U灯=
| E | ||
R+
|
联立②④⑤⑥得 UMN=20V ⑦
(3)设金属棒克服安培力做功为W,由动能定理得 Pt-W=
| 1 |
| 2 |
克服安培力做功转化为总电能,设为Q,则有Q=W ⑨
故灯泡发热为Q1=
| R | ||
R+
|
联立⑧⑨⑩得:Q1=12J
答:(1)若施加的水平恒力F=8N,则金属棒达到的稳定速度为6m/s;
(2)在(1)的前提下,金属棒MN两端的电势差UMN为20V;
(3)灯泡产生的热量是12J.
点评:解决本题关键通过受力判断出金属棒的运动情况,知道当金属棒加速度为零时,速度最大.以及会根据能量守恒定律或动能定理求出整个电路上产生的电热能.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
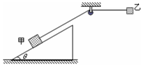 (2013?广东模拟)如图,甲和斜面均静止.现用细绳通过定滑轮连接甲乙,将乙拉至水平,绳子处于自然伸直状态,释放乙后甲和斜面仍然静止,不计滑轮摩擦.则乙下落到最低点过程中( )
(2013?广东模拟)如图,甲和斜面均静止.现用细绳通过定滑轮连接甲乙,将乙拉至水平,绳子处于自然伸直状态,释放乙后甲和斜面仍然静止,不计滑轮摩擦.则乙下落到最低点过程中( )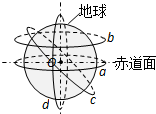 (2013?广东模拟)如图,O是地球球心,下列说法正确的是( )
(2013?广东模拟)如图,O是地球球心,下列说法正确的是( ) (2013?广东模拟)如图在研究光电效应的实验中,发现用一定频率的A单色光照射光电管时,电流表指针会发生偏转,而用另一频率的B单色光照射时不发生光电效应,则下列说法正确的是( )
(2013?广东模拟)如图在研究光电效应的实验中,发现用一定频率的A单色光照射光电管时,电流表指针会发生偏转,而用另一频率的B单色光照射时不发生光电效应,则下列说法正确的是( )