题目内容
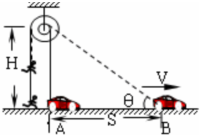 摄影组在某大楼边拍摄武打片,要求特技演员从地面竖直飞到高处如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,绕在轮上的细钢丝将特技演员拉起,则在此过程中特技演员( )
摄影组在某大楼边拍摄武打片,要求特技演员从地面竖直飞到高处如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,绕在轮上的细钢丝将特技演员拉起,则在此过程中特技演员( )分析:利用几何关系求出钢丝上升的距离,根据轮和轴的具有相同的角速度,求出演员上升的距离,再去求解重力做功.
根据速度的分解求出钢丝的速度和轨道车的速度的关系.运用动能定理研究求解.
根据速度的分解求出钢丝的速度和轨道车的速度的关系.运用动能定理研究求解.
解答:解:A、由图可知,在这一过程中,连接轨道车的钢丝上升的距离为
h0=
-H=2m
轮和轴的直径之比为2:1.
所以演员上升的距离为h=2×2m=4m
此过程中特技演员重力做功WG=-mgh=-2000J,所以克服重力做功2000J.故A错误.
B、设轨道车在B时细线与水平方向之间的夹角为θ,将此时轨道车的速度分解,此时钢丝的
v丝=vcosθ=
=3m/s,
由于轮和轴的角速度相同,则其线速度之比等于半径(直径)之比为2:1,
v人=2v丝=6m/s
根据动能定理得:
合力做功W合=△Ek=900J,故B错误.
C、根据动能定理得:
合力做功W合=△Ek=WG+W拉.
W拉=mgh+
mv人2=2900J.故C正确.
D、根据功能关系可知,钢丝在一过程中对演员做的功等于演员机械能的增量,即
△E=W拉=2900J,所以机械能增加2900J,故D错误.
故选:C.
h0=
| s2+H2 |
轮和轴的直径之比为2:1.
所以演员上升的距离为h=2×2m=4m
此过程中特技演员重力做功WG=-mgh=-2000J,所以克服重力做功2000J.故A错误.
B、设轨道车在B时细线与水平方向之间的夹角为θ,将此时轨道车的速度分解,此时钢丝的
v丝=vcosθ=
| vs | ||
|
由于轮和轴的角速度相同,则其线速度之比等于半径(直径)之比为2:1,
v人=2v丝=6m/s
根据动能定理得:
合力做功W合=△Ek=900J,故B错误.
C、根据动能定理得:
合力做功W合=△Ek=WG+W拉.
W拉=mgh+
| 1 |
| 2 |
D、根据功能关系可知,钢丝在一过程中对演员做的功等于演员机械能的增量,即
△E=W拉=2900J,所以机械能增加2900J,故D错误.
故选:C.
点评:注意点:1、轮和轴的角速度相同,根据轮和轴的直径之比知道线速度关系.
2、掌握速度分解找出分速度和合速度的关系.
2、掌握速度分解找出分速度和合速度的关系.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
摄影组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶如图所示。若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴 , 轮和轴的直径之比为2:1。若轨道车从图中A前进s=6m到B处时速度为v=5m/s,则由于绕在轮上细钢丝拉动特技演员(以地面为零重力势能面)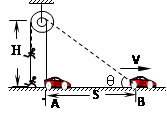

| A.上升的高度为4m |
| B.在最高点具有竖直向上的速度3m/s |
| C.在最高点具有的机械能为2900J |
| D.钢丝在这一过程中对演员做的功为1225J |
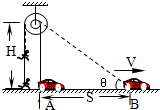 摄影组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,则由于绕在轮上细刚丝拉动特技演员( )
摄影组在某大楼边拍摄武打片,要求特技演员从地面飞到屋顶如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,则由于绕在轮上细刚丝拉动特技演员( )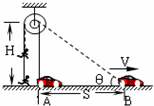 摄影组在某大楼边拍摄武打片,要求特技演员从地面竖直飞到高处如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,绕在轮上细刚丝将特技演员拉起,则在此过程中特技演员( )
摄影组在某大楼边拍摄武打片,要求特技演员从地面竖直飞到高处如图所示.若特技演员的质量m=50kg,人和车均视为质点,g=10m/s2,导演从某房顶离地H=8m处架设了轮轴,轮和轴的直径之比为2:1.若轨道车从图中A前进s=6m到B处时速度为v=5m/s,绕在轮上细刚丝将特技演员拉起,则在此过程中特技演员( )
