题目内容
16.(1)在利用单摆测定重力加速度的实验中.若测得的g值偏大.可能的原因是:DA.摆球质量过大
B.单摆振动时振幅较小
C.测量摆长时.只考虑了线长.忽略了小球的半径
D.测量周期时.把n个全振动误认为(n+1)个全振动.使周期偏小
E.测量周期时.把n个全振动误认为(n-1)个全振动.使周期偏大
(2)若单摆是一个秒摆.将此摆移到月球上.(g月=$\frac{1}{6}$g地).其周期是2$\sqrt{6}$s
(3)实验中游标尺(50分度)和秒表的读数如图.分别是6.88mm.70.8s.

分析 (1)根据单摆周期公式求出重力加速度表达式,然后根据该表达式分析答题.
(2)应用单摆周期公式分析答题.
(3)游标卡尺主尺与游标尺示数之和是游标卡尺的示数;秒表分针与秒针的示数之和是秒表示数
解答 解:(1)由单摆周期公式T=2π$\sqrt{\frac{L}{g}}$可知,重力加速度g=$\frac{4{π}^{2}L}{{T}^{2}}$;
A、由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,重力加速度与摆球质量无关,故A错误;
B、由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,重力加速度与单摆振动的振幅无关,故B错误;
C、测量摆长时,只考虑了线长,忽略了小球的半径,摆长L偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,所测重力加速度偏小,故C错误;
D、测量周期时,把n个全振动误认为(n+1)个全振动,使周期偏小,由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,所测重力加速度偏大,故D正确;
E、测量周期时,把n个全振动误认为(n-1)个全振动,使周期偏大,由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,所测重力加速度偏小,故E错误;
故选:D.
(2)秒摆的周期T=2s,将秒摆移到月球上,其周期T′=2π$\sqrt{\frac{L}{{g}_{月}}}$=2π$\sqrt{\frac{L}{\frac{{g}_{地}}{6}}}$=$\sqrt{6}$T=2$\sqrt{6}$ s.
(3)由图示游标卡尺可知,主尺示数为6mm,游标尺示数为44×0.02mm=0.88mm,
则游标卡尺示数为6mm+0.88mm=6.88mm;
由图示秒表可知,分针示数为1min=60s,秒针示数为10.8s,则秒表示数为60s+10.8s=70.8s.
故答案为:(1)D; (2)2$\sqrt{6}$s;(3)6.88,70.8.
点评 本题考查了单摆周期公式的应用、游标卡尺与秒表的读数问题,掌握基础知识即可正确解题,本题难度不大.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
| A. | 3、2 | B. | 3、4 | C. | 4、3 | D. | 5、4 |
| A. | 向心加速度的方向始终与速度的方向垂直 | |
| B. | 向心加速度的方向保持不变 | |
| C. | 在匀速圆周运动中,向心加速度是恒定的 | |
| D. | 在匀速圆周运动中,向心加速度的大小不断变化 |
| A. | 振子的速度 | B. | 振子的加速度 | C. | 振子的回复力 | D. | 振子的动能 |
| A. | 乙分子的动能变化量为$\frac{1}{2}$mv2 | |
| B. | 分子力对乙分子做的功为$\frac{1}{2}$mv2 | |
| C. | 分子引力比分子斥力多做了$\frac{1}{2}$mv2的功 | |
| D. | 分子斥力比分子引力多做了$\frac{1}{2}$mv2的功 |
 在如图所示的电路中,开关S1、S2、S3、S4均闭合,C是两极板水平放置的平行板电容器,板间悬浮着一带电油滴P.则下列措施中能使油滴P一定向下运动的是( )
在如图所示的电路中,开关S1、S2、S3、S4均闭合,C是两极板水平放置的平行板电容器,板间悬浮着一带电油滴P.则下列措施中能使油滴P一定向下运动的是( )| A. | 断开S1增大电容器极板间的距离 | |
| B. | 断开S2,同时减小电容器两极板间的距离 | |
| C. | 断开S3,同时增大电容器两极板间的距离 | |
| D. | 断开S4,同时增大电容器两极板间的距离 |
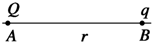 场源电荷Q=2×10-4C,是正点电荷.检验电荷q=-2×10-5C,是负点电荷,它们相距r=2m,且都在真空中,如图所示.求:
场源电荷Q=2×10-4C,是正点电荷.检验电荷q=-2×10-5C,是负点电荷,它们相距r=2m,且都在真空中,如图所示.求: 如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态.已知金属棒长L=0.1m,质量m=0.05kg,棒中通有I=10A的向右的电流,取g=10m/s2.
如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态.已知金属棒长L=0.1m,质量m=0.05kg,棒中通有I=10A的向右的电流,取g=10m/s2.