题目内容
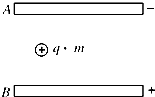 如图,A、B为两块水平放置的带等量异种电荷的平行金属板,一个质量m=10-4 kg,电荷量q=5×10-5 C的带正电粒子静止于两板的正中央,已知两板间距离为20cm,g=10m/s2,求:
如图,A、B为两块水平放置的带等量异种电荷的平行金属板,一个质量m=10-4 kg,电荷量q=5×10-5 C的带正电粒子静止于两板的正中央,已知两板间距离为20cm,g=10m/s2,求:(1)两板间匀强电场的场强大小;
(2)两板间的电势差;
(3)若用某种方法将带电粒子的带电荷量减少一半,使带电粒子从两板正中央由静止开始运动,则经过多长时间粒子撞到板上.
分析:A、B为两块水平放置的带等量异种电荷的平行金属板,极板内部为匀强电场,根据带电粒子静止于板正中央,带点离子所受重力与电场力等大反向,即可求极板的场强;根据E=
可求两板间的电势差;若用某种方法将带电粒子的带电荷量减少一半,带电粒子所受重力不变,电场力变为原来的一半(方向不变),所以求出带电离子的合力,根据牛顿第二定律F=ma和x=
at2可求离子撞到极板的时间.
| U |
| d |
| 1 |
| 2 |
解答:解:(1)带电粒子静止于板正中央,所以mg=Eq,即:E=
=
=20V/m.
(2)根据匀强电场:U=Ed=20V/m×0.02m=4v.
(3)若用某种方法将带电粒子的带电荷量减少一半,带电粒子所受重力不变,电场力变为原来的一半(方向不变),所以:F合=
mg…①
由牛顿第二定律得:F合=ma…②
带电粒子从两板正中央由静止开始运动,则经过t时间粒子撞到板上,则:
=
at2…③
联立①②③解之得:t=0.2s
答:(1)两板间匀强电场的场强为20 V/m
(2)两板间的电势差为4 V
(3)若用某种方法将带电粒子的带电荷量减少一半,使带电粒子从两板正中央由静止开始运动,则经过0.2撞到板上.
| mg |
| q |
| 10-4Kg×10m/s2 |
| 5×10-5C |
(2)根据匀强电场:U=Ed=20V/m×0.02m=4v.
(3)若用某种方法将带电粒子的带电荷量减少一半,带电粒子所受重力不变,电场力变为原来的一半(方向不变),所以:F合=
| 1 |
| 2 |
由牛顿第二定律得:F合=ma…②
带电粒子从两板正中央由静止开始运动,则经过t时间粒子撞到板上,则:
| d |
| 2 |
| 1 |
| 2 |
联立①②③解之得:t=0.2s
答:(1)两板间匀强电场的场强为20 V/m
(2)两板间的电势差为4 V
(3)若用某种方法将带电粒子的带电荷量减少一半,使带电粒子从两板正中央由静止开始运动,则经过0.2撞到板上.
点评:根据带电粒子静止,寻求重力和电场力大小相等是解题的关键;灵活应用E=
、F=ma和匀变速直线的运动规律是突破点.
| U |
| d |

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
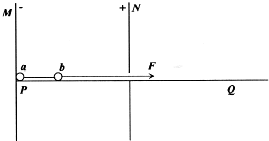 如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的
如图所示,MN是两块竖直放置的带电平行板,板内有水平向左的匀强电场,PQ是光滑绝缘的水平滑槽,滑槽从N板中间穿入电场.a、b为两个带等量正电荷的相同小球,两球之间用绝缘水平轻杆固连,轻杆长为两板间距的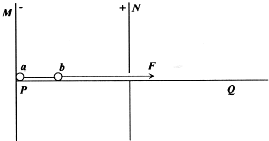
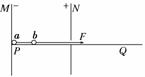
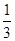 ,杆长远大于球的半径,开始时从外面用绝缘轻绳拉着b球使a球靠近M板但不接触。现对轻绳施以沿杆方向的水平恒力拉着b球和a球由静止向右运动,当b球刚从小孔离开电场时,撤去拉力,之后a球也恰好能离开电场。求运动过程中b球离开电场前和离开电场后(a球还在电场中)轻杆中的弹力之比。不计两球间库仑力,球视为点电荷。
,杆长远大于球的半径,开始时从外面用绝缘轻绳拉着b球使a球靠近M板但不接触。现对轻绳施以沿杆方向的水平恒力拉着b球和a球由静止向右运动,当b球刚从小孔离开电场时,撤去拉力,之后a球也恰好能离开电场。求运动过程中b球离开电场前和离开电场后(a球还在电场中)轻杆中的弹力之比。不计两球间库仑力,球视为点电荷。