题目内容
小轿车以20m/s的速度在平直公路上匀速行驶,司机突然发现正前方有个收费站,经20s后司机才刹车使车匀减速恰停在缴费窗口,缴费后匀加速到20m/s后继续匀速前行.已知小轿车刹车时的加速度为2m/s2,停车缴费所用时间为30s,启动时加速度为1m/s2.(1)司机是在离收费窗口多远处发现收费站的.
(2)因国庆放假期间,全国高速路免费通行,小轿车可以不停车通过收费站,但要求轿车通过收费窗口前9m区间速度不超过6m/s,则国庆期间该小轿车应离收费窗口多远处开始刹车?因不停车通过可以节约多少时间?
【答案】分析:1、解出匀速运动的位移,再解出匀减速运动的位移,两位移相加即为要求的距离.
2、分段研究,收费时总时间为:减速到0的时间,加上收费的时间,再加上加速到20m/s的时间.
不收费时的总时间为:减速到6m/s的时间,加上匀速运动的时间,加上加速到20m/s的时间,还要加上匀速运动的时间.
上述时间的差值即为节约的时间.
解答:解:(1)根据题意,设司机匀速运动位移为 s1;减速运动时间为t2,位移为s2.
s1=vt=20×20=400(m)
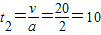 (s)
(s)
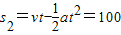 (m)
(m)
所以司机在离收费站窗口100+400=500m处发现收费站的.
(2)根据题意轿车应该在收费窗口前9m处速度减为6m/s,设车减速位移为s1′,
由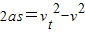 得:
得:
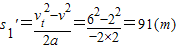
所以,轿车应离收费窗口91+9=100(m)处开始刹车.
设停车收费后加速时间为t3,位移为s3,则有: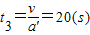
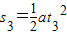 =200(m)
=200(m)
若停车收费经过窗口前100m到窗后200m的总时间为:t1+t2+t3=10+30+20=60(s)
若不停车收费也是窗前100m开始刹车,时间为: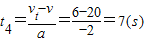
窗口前匀速时间:
窗口后加速到20m/s所用时间为:
加速运动的位移由: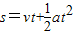 得:
得: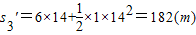
窗口后还有200-182=18(m)匀速运动,其时间为: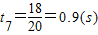
若不停车经过窗口前100m到窗口后200m的总时间为:t4+t5+t6+t7=7+1.5+14+0.9=23.4(s)
所以不停车通过可以节约时间为60-23.4=36.6(s)的时间.
答:(1)司机是在离收费窗口500m发现收费站的.
(2)国庆期间该小轿车应离收费窗口100m开始刹车.因不停车通过可以节约36.6s.
点评:此题运动的过程复杂,轿车经历减速、匀速、加速,加速度、位移、时间等都不一样.分析这样的问题时,要能在草稿子上画一画运动的过程图,找出空间关系,有助于解题.此题有一定的难度,是一道好题.
2、分段研究,收费时总时间为:减速到0的时间,加上收费的时间,再加上加速到20m/s的时间.
不收费时的总时间为:减速到6m/s的时间,加上匀速运动的时间,加上加速到20m/s的时间,还要加上匀速运动的时间.
上述时间的差值即为节约的时间.
解答:解:(1)根据题意,设司机匀速运动位移为 s1;减速运动时间为t2,位移为s2.
s1=vt=20×20=400(m)
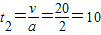 (s)
(s)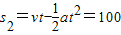 (m)
(m)所以司机在离收费站窗口100+400=500m处发现收费站的.
(2)根据题意轿车应该在收费窗口前9m处速度减为6m/s,设车减速位移为s1′,
由
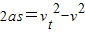 得:
得: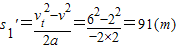
所以,轿车应离收费窗口91+9=100(m)处开始刹车.
设停车收费后加速时间为t3,位移为s3,则有:
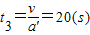
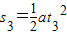 =200(m)
=200(m)若停车收费经过窗口前100m到窗后200m的总时间为:t1+t2+t3=10+30+20=60(s)
若不停车收费也是窗前100m开始刹车,时间为:
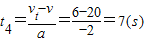
窗口前匀速时间:

窗口后加速到20m/s所用时间为:

加速运动的位移由:
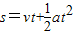 得:
得: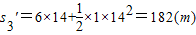
窗口后还有200-182=18(m)匀速运动,其时间为:
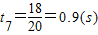
若不停车经过窗口前100m到窗口后200m的总时间为:t4+t5+t6+t7=7+1.5+14+0.9=23.4(s)
所以不停车通过可以节约时间为60-23.4=36.6(s)的时间.
答:(1)司机是在离收费窗口500m发现收费站的.
(2)国庆期间该小轿车应离收费窗口100m开始刹车.因不停车通过可以节约36.6s.
点评:此题运动的过程复杂,轿车经历减速、匀速、加速,加速度、位移、时间等都不一样.分析这样的问题时,要能在草稿子上画一画运动的过程图,找出空间关系,有助于解题.此题有一定的难度,是一道好题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目