题目内容
[物理一选修3一4]
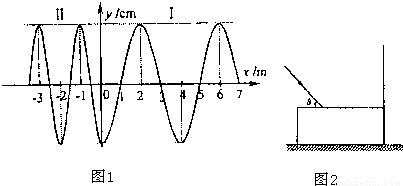
(1)图1中y轴是两种不同介质I、Ⅱ的分界面,一波源以坐标系原点为中心沿y轴上下振动,形成的两列简谐波分别沿+x轴和-x轴方向传播,某一时刻的波形如图所示.在介质I、Ⅱ中传播的波
A.周期之比为2:1
B.波长之比为l:2
C.波速之比为2:1
D.经过相同的时间,波在介质I、Ⅱ中传播距离之比为1:2
(2)如图2所示,上下表面平行的玻璃砖,折射率为n=
,下表面镀有银反射面.一束单色光与界面的夹角θ=45°射到玻璃表面上,结果在玻璃砖右边竖直光屏上出现相距h=2.0cm的光点A和B(图中未画出A、B).
①请在图中画出光路示意图;
②求玻璃砖的厚度d.
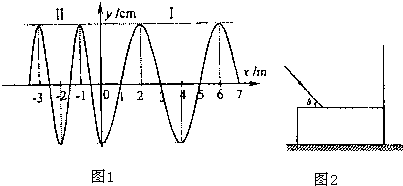
(1)图1中y轴是两种不同介质I、Ⅱ的分界面,一波源以坐标系原点为中心沿y轴上下振动,形成的两列简谐波分别沿+x轴和-x轴方向传播,某一时刻的波形如图所示.在介质I、Ⅱ中传播的波
C
C
;A.周期之比为2:1
B.波长之比为l:2
C.波速之比为2:1
D.经过相同的时间,波在介质I、Ⅱ中传播距离之比为1:2
(2)如图2所示,上下表面平行的玻璃砖,折射率为n=
| 2 |
①请在图中画出光路示意图;
②求玻璃砖的厚度d.

分析:(1)同一波源产生的波频率相同,根据波动图象读出波长之比,再确定波速之比.
(2)①入射光一部分在玻璃砖一表面反射,另一部分折射进入玻璃砖后在下表面反射后,再折射进入空气,画出光路图.②根据折射定律求出光线第一次在玻璃砖上表面折射时的折射角,以及第二次折射的折射角,由几何知识求出玻璃砖的厚度.
(2)①入射光一部分在玻璃砖一表面反射,另一部分折射进入玻璃砖后在下表面反射后,再折射进入空气,画出光路图.②根据折射定律求出光线第一次在玻璃砖上表面折射时的折射角,以及第二次折射的折射角,由几何知识求出玻璃砖的厚度.
解答:解: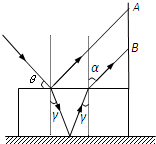 (1)A、两列简谐波是由同波源产生的,周期相同.故A错误.
(1)A、两列简谐波是由同波源产生的,周期相同.故A错误.
B、由图读出I、Ⅱ中传播的波波长分别为λⅠ=4m和λⅡ=2m,波长之比为λⅠ:λⅡ=2:1.故B错误.
C、由波速公式v=
,T相同,则波速之比为vⅠ:vⅡ=λⅠ:λⅡ=2:1.故C正确.
D、波在同一介质中匀速传播,波在介质中传播距离S=vt,则经过相同的时间,波在介质I、Ⅱ中传播距离之比为S1:S2=v1:v2=2:1.故D错误.
故选C
(2)①光路图如图示
(2)设第一次折射时折射角为r.则有:n=
解得:r=30°
设第二次折射时折射角为α,则有:
=
解得:α=45°
由几何关系得:h=2dtanr
d=
=
=
cm
答:
①在图中画出光路示意图如图;
②玻璃砖的厚度
cm.
 (1)A、两列简谐波是由同波源产生的,周期相同.故A错误.
(1)A、两列简谐波是由同波源产生的,周期相同.故A错误.B、由图读出I、Ⅱ中传播的波波长分别为λⅠ=4m和λⅡ=2m,波长之比为λⅠ:λⅡ=2:1.故B错误.
C、由波速公式v=
| λ |
| T |
D、波在同一介质中匀速传播,波在介质中传播距离S=vt,则经过相同的时间,波在介质I、Ⅱ中传播距离之比为S1:S2=v1:v2=2:1.故D错误.
故选C
(2)①光路图如图示
(2)设第一次折射时折射角为r.则有:n=
| sin(90°-θ) |
| sinr |
解得:r=30°
设第二次折射时折射角为α,则有:
| sinr |
| sinα |
| 1 |
| n |
解得:α=45°
由几何关系得:h=2dtanr
d=
| h |
| 2tanr |
| 2 |
| 2tan30° |
| 3 |
答:
①在图中画出光路示意图如图;
②玻璃砖的厚度
| 3 |
点评:波的频率等于波源的振动频率,由波源的振动情况决定,与介质无关.几何光学要画出光路图.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 [物理一选修3-4]
[物理一选修3-4]
 s这个时刻
s这个时刻 ,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.请画出光路图,并求两个光斑之间的距离L.
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃砖的圆心O,结果在水平屏幕MN上出现两个光斑.请画出光路图,并求两个光斑之间的距离L.


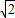 ,下表面镀有银反射面.一束单色光与界面的夹角θ=45°射到玻璃表面上,结果在玻璃砖右边竖直光屏上出现相距h=2.0cm的光点A和B(图中未画出A、B).
,下表面镀有银反射面.一束单色光与界面的夹角θ=45°射到玻璃表面上,结果在玻璃砖右边竖直光屏上出现相距h=2.0cm的光点A和B(图中未画出A、B).