题目内容
 (2007?海淀区模拟)如图所示,A、B为两个半径相同的小球,A的质量M=0.60kg,B的质量m=0.40kg,A球用轻质细绳吊起,绳长l=1.0m(两球的半径大小可忽略不计),B球放在悬点正下方的光滑水平桌面的边缘,开始时两球相互接触但没有作用力.现将A球拉到高h=0.20m处由静止释放,摆到最低点时与B球碰撞,碰后两球粘在一起共同向上摆.若g取10m/s2,求:
(2007?海淀区模拟)如图所示,A、B为两个半径相同的小球,A的质量M=0.60kg,B的质量m=0.40kg,A球用轻质细绳吊起,绳长l=1.0m(两球的半径大小可忽略不计),B球放在悬点正下方的光滑水平桌面的边缘,开始时两球相互接触但没有作用力.现将A球拉到高h=0.20m处由静止释放,摆到最低点时与B球碰撞,碰后两球粘在一起共同向上摆.若g取10m/s2,求:(1)A球刚接触到B球时的速度大小;
(2)两小球相碰撞过程中,B球对A球所做的功;
(3)两小球碰撞后一起运动离开桌面的瞬间,两球对细绳的拉力大小.
分析:(1)小球下摆过程机械能守恒,由机械能守恒定律可以求出碰前的速度.
(2)碰撞过程动量守恒,由动量守恒定律与动能定律可以求出B对A做的功.
(3)由牛顿第二定律可以求出球受到的拉力,然后由牛顿第三定律求出球对绳子的作用力.
(2)碰撞过程动量守恒,由动量守恒定律与动能定律可以求出B对A做的功.
(3)由牛顿第二定律可以求出球受到的拉力,然后由牛顿第三定律求出球对绳子的作用力.
解答:解:(1)A球下摆过程中,机械能守恒,设其刚与B球碰撞时的速度大小为vA,
由机械能守恒定律得:Mgh=
MvA2 ,解得vA=
=2.0m/s;
(2)两球相碰撞的过程,系统沿水平方向动量守恒,
设碰撞后的共同速度大小为v,由动量守恒定律得:
MvA=(M+m)v,解得:v=1.2m/s,
由动能定理得:B球对A球所做的功:W=
M(v2-vA2)=-0.77J;
(3)设两球碰撞后一起运动离开桌面的瞬间所受细绳的拉力为T,
两球碰撞后的瞬间,由牛顿第二定律得:T-(M+m)g=(M+m)
,
解得:T=11.44N,
根据牛顿第三定律可知,两球对细绳的拉力大小T′=11.44N;
答:(1)A球刚接触到B球时的速度大小为2m/s;
(2)两小球相碰撞过程中,B球对A球所做的功为0.77J;
(3)两小球碰撞后一起运动离开桌面的瞬间,两球对细绳的拉力大小为11.44N.
由机械能守恒定律得:Mgh=
| 1 |
| 2 |
| 2gh |
(2)两球相碰撞的过程,系统沿水平方向动量守恒,
设碰撞后的共同速度大小为v,由动量守恒定律得:
MvA=(M+m)v,解得:v=1.2m/s,
由动能定理得:B球对A球所做的功:W=
| 1 |
| 2 |
(3)设两球碰撞后一起运动离开桌面的瞬间所受细绳的拉力为T,
两球碰撞后的瞬间,由牛顿第二定律得:T-(M+m)g=(M+m)
| v2 |
| l |
解得:T=11.44N,
根据牛顿第三定律可知,两球对细绳的拉力大小T′=11.44N;
答:(1)A球刚接触到B球时的速度大小为2m/s;
(2)两小球相碰撞过程中,B球对A球所做的功为0.77J;
(3)两小球碰撞后一起运动离开桌面的瞬间,两球对细绳的拉力大小为11.44N.
点评:分析清楚物体运动过程,应用机械能守恒定律、动量守恒定律、动能定理、牛顿运动定律即可正确解题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
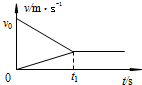 (2007?海淀区一模)长木板A放在光滑的水平面上,质量为m的物块B以水平初速度v0从A的一端滑上A的水平上表面,它们在运动过程中的v-t图线如图所示.则根据图中所给出的已知数据v0、t1及物块质量m,能够求出的物理量是( )
(2007?海淀区一模)长木板A放在光滑的水平面上,质量为m的物块B以水平初速度v0从A的一端滑上A的水平上表面,它们在运动过程中的v-t图线如图所示.则根据图中所给出的已知数据v0、t1及物块质量m,能够求出的物理量是( ) (2007?海淀区一模)振源以原点O为平衡位置,沿y轴方向做简谐运动,它激发的简谐波在x轴上沿正负两个方向传播,在某一时刻沿x轴正向传播的波形如图所示.如图所示的各个质点中,振动情况始终与原点的左方的质点P的振动情况相同的是( )
(2007?海淀区一模)振源以原点O为平衡位置,沿y轴方向做简谐运动,它激发的简谐波在x轴上沿正负两个方向传播,在某一时刻沿x轴正向传播的波形如图所示.如图所示的各个质点中,振动情况始终与原点的左方的质点P的振动情况相同的是( )