题目内容
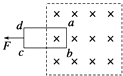
【题目】如图，一质量为m，长度为l的均匀柔软细绳PQ竖直悬挂．用外力将绳的下端Q缓慢地竖直向上拉起至M点，M点与绳的上端P相距 
l．重力加速度大小为g．在此过程中，外力做的功为（ ）
A.
mgl
B.
mgl
C.
mgl
D.
mgl
【答案】A
【解析】根据功能关系可知，拉力所做的功等于MQ段系统重力势能的增加量；对MQ分析，设Q点为零势能点，则可知，MQ段的重力势能为EP1= 
× 
= 
；
将Q点拉至M点时，重心离Q点的高度h= 
+ = 
，故重力势能EP2═ × = 
因此可知拉力所做的功W=EP2﹣EP1= 
mgl，故A正确，BCD错误．
故选：A．
【考点精析】本题主要考查了功能关系的相关知识点，需要掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1才能正确解答此题．
【题目】利用如图1所示的实验装置探究恒力做功与物体动能变化的关系．小车的质量为M=200.0g，钩码的质量为m=10.0g，打点计时器的电源为50Hz的交流电．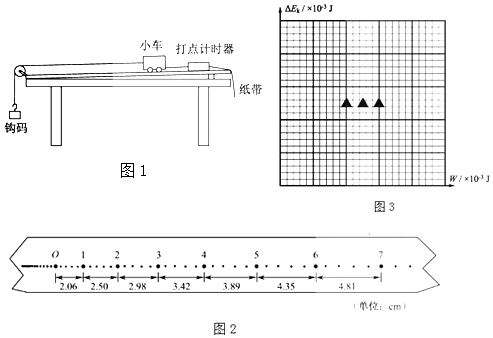
（1）挂钩码前，为了消除摩擦力的影响，应调节木板右侧的高度，直至向左轻推小车观察到 ．
（2）挂上钩码，按实验要求打出的一条纸带如图2所示．选择某一点为O，一次每隔4个计时点取一个计数点．用刻度尺量出相邻计数点间的距离△x，记录在纸带上．计算打出各计数点时小车的速度v，其中打出计数点“1”时小车的速度v1=m/s．
（3）将钩码的重力视为小车受到的拉力，取g=9.80m/s2 ， 利用W=mg△x算出拉力对小车做的功W．利用Ek= 
Mv2算出小车动能，并求出动能的变化量△Ek ． 计算结果见下表．
W/×10﹣3J | 2.45 | 2.92 | 3.35 | 3.81 | 4.26 |
△Ek/×10﹣3J | 2.31 | 2.73 | 3.12 | 3.61 | 4.00 |
请根据表中的数据，在答题卡的方格纸上作出△Ek﹣W图象．
（4）实验结果表明，△Ek总是略小于W．某同学猜想是由于小车所受拉力小于钩码重力造成的．用题中小车和钩码质量的数据可算出小车受到的实际拉力F= ．
