题目内容
 一条圆柱形的光导纤维长为L、折射率为n,光在真空中的传播速度为c,求:光从它的一端端面的圆心射入,经全反射后从另一端射出,所需的最长时间t.
一条圆柱形的光导纤维长为L、折射率为n,光在真空中的传播速度为c,求:光从它的一端端面的圆心射入,经全反射后从另一端射出,所需的最长时间t.分析:根据全反射条件,依据光的折射定律,结合几何关系,即可求解.
解答:解:如图,设进入光纤的光线射在边界时的入射角为θ,要发生全反射则θ≥C,
C为光线的临界角光在光纤中运行的时间为:t=
由此可得时间最长时:θ=C
又由 sinC=
因v=
联立上述各式,解得 t=
答:所需的最长时间得
.
C为光线的临界角光在光纤中运行的时间为:t=
| ||
| v |
由此可得时间最长时:θ=C
又由 sinC=
| 1 |
| n |
因v=
| c |
| n |
联立上述各式,解得 t=
| n2L |
| c |
答:所需的最长时间得
| n2L |
| c |
点评:考查光的全反射条件,掌握光的折射定律,理解sinC=
公式的含义,知道最长时间时,入射角恰好等于临界角.
| 1 |
| n |

练习册系列答案
相关题目
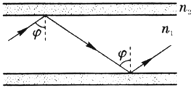 据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为1,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法中正确的是( )(图中所标的φ为全反射的临界角)
据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为1,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法中正确的是( )(图中所标的φ为全反射的临界角)A、n1>1,t=
| ||||
B、n1>1,t=
| ||||
C、n1<1,t=
| ||||
D、n1<1,t=
|
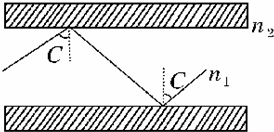 2010年广州亚运会,光纤通信网覆盖了所有奥运场馆,为各项比赛提供安全可靠的通信服务,光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯折射率为n1,外层材料的折射率为n2,光从一端射入经全反射后从另一端射出所需的最长时间为t,请探究分析以下问题:
2010年广州亚运会,光纤通信网覆盖了所有奥运场馆,为各项比赛提供安全可靠的通信服务,光纤通信利用光的全反射将大量信息高速传输.如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯折射率为n1,外层材料的折射率为n2,光从一端射入经全反射后从另一端射出所需的最长时间为t,请探究分析以下问题:
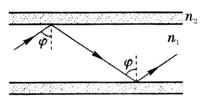 据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输。如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法中正确的是( )(图中所标的
据报道:2008年北京奥运会,光纤通信网将覆盖所有奥运场馆,为各项比赛提供安全可靠的通信服务.光纤通信利用光的全反射将大量信息高速传输。如图所示,一条圆柱形的光导纤维,长为L,它的玻璃芯的折射率为n1,外层材料的折射率为n2,光在空气中的传播速度为c,若光从它的一端射入经全反射后从另一端射出所需的最长时间为t,则下列说法中正确的是( )(图中所标的