题目内容
13. 如图所示的正方形区域,在区域内没有磁场的情况下,带电粒子(不计重力)以某一初速度从AB边中点垂直于该边方向射入时,穿过此区域的时间为t,若在该区域加一垂直纸面向里的匀强磁场,带电粒子仍从同一位置以同一速度射入,粒子从C点射出.若只有时间t为已知量,根据上述条件
如图所示的正方形区域,在区域内没有磁场的情况下,带电粒子(不计重力)以某一初速度从AB边中点垂直于该边方向射入时,穿过此区域的时间为t,若在该区域加一垂直纸面向里的匀强磁场,带电粒子仍从同一位置以同一速度射入,粒子从C点射出.若只有时间t为已知量,根据上述条件(1)确定带电粒子的带电性质
(2)求出带电粒子在匀强磁场中的运动时间.
分析 (1)粒子受洛伦兹力向下,根据左手定则判断粒子的电性;
(2)画出运动轨迹,结合几何关系求解出轨道半径,然后根据牛顿第二定律列式求解时间.
解答 解:(1)加上磁场时,磁感应强度向内,粒子的速度向右,洛伦兹力向下,根据左手定则,粒子带负电荷;
(2)没有加磁场时,粒子是匀速直线运动,设正方形区域的边长为a,有:
t=$\frac{a}{v}$
加上磁场后,粒子做匀速圆周运动,轨迹如图所示:
结合几何关系,有:
${r}^{2}={a}^{2}+(r-\frac{a}{2})^{2}$
解得:
r=$\frac{5}{4}$a
故sinθ=$\frac{a}{r}$=0.8,故θ=53°
根据牛顿第二定律,有:
qvB=m$\frac{{v}^{2}}{r}$
粒子在磁场中运动时间:
t′=$\frac{53°}{360°}\frac{2πm}{qB}$
联立解得:
t′=$\frac{53π}{144}t$
答:(1)粒子带负电荷;
(2)带电粒子在匀强磁场中的运动时间为$\frac{53π}{144}t$.
点评 本题关键是明确粒子的运动性质,画出轨迹,结合几何关系得到轨道半径,然后根据牛顿第二定律列式求解,基础题目.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
4.下列说法中正确的是( )
| A. | 知道水蒸气的摩尔体积和水分子的体积,不能计算出阿伏加德罗常数 | |
| B. | 硬币或钢针能浮于水面上,是由于液体表面张力的作用 | |
| C. | 晶体有固定的熔点,具有规则的几何外形,物理性质具有各向异性 | |
| D. | 影响蒸发快慢以及影响人们对干爽与潮湿感受的因素是空气中水蒸气的压强与同一温度下水的饱和汽压的差距 | |
| E. | 随着科技的发展,将来可以利用高科技手段,将散失在环境中的内能重新收集起来加以利用而不引起其他变化 |
8. 高中学业水平测试体育考场上某同学掷出的铅球运动轨迹如图所示,A点为抛出点,E点为落地点,B点为最高点,运动过程空气阻力大小与速度平方成正比,与速度反向,则下列说法正确的是( )
高中学业水平测试体育考场上某同学掷出的铅球运动轨迹如图所示,A点为抛出点,E点为落地点,B点为最高点,运动过程空气阻力大小与速度平方成正比,与速度反向,则下列说法正确的是( )
 高中学业水平测试体育考场上某同学掷出的铅球运动轨迹如图所示,A点为抛出点,E点为落地点,B点为最高点,运动过程空气阻力大小与速度平方成正比,与速度反向,则下列说法正确的是( )
高中学业水平测试体育考场上某同学掷出的铅球运动轨迹如图所示,A点为抛出点,E点为落地点,B点为最高点,运动过程空气阻力大小与速度平方成正比,与速度反向,则下列说法正确的是( )| A. | A点的加速度比B点的加速度大 | |
| B. | 运动过程中B点动能最大 | |
| C. | E点机械能最大 | |
| D. | 若没有空气阻力,铅球的最高点将会比B高 |
18.手提电脑散热底座一般设置有四个卡位来调节角度,如图甲所示,某同学将电脑放在散热底座上,为了获得更好的舒适度,由原卡位1调至卡位4(如图乙),手提电脑始终处于静止状态,则( )


| A. | 电脑受到的支持力变小 | |
| B. | 电脑受到的摩擦力变大 | |
| C. | 散热底座对电脑作用力的合力不变 | |
| D. | 电脑受到的支持力与摩擦力的大小之和等于其重力 |
5.关于牛顿第一定律,以下说法错误的是( )
| A. | 伽利略的理想斜面实验是牛顿第一定律的”实验“基础 | |
| B. | 牛顿第一定律可以用真实的实验进行验证 | |
| C. | 牛顿第一定律表明一切物体都具有惯性 | |
| D. | 牛顿第一定律是牛顿物理学的基石 |
2.下列说法中正确的是( )
| A. | 电场强度为零的点,电势一定为零 | |
| B. | 电场强度处处相等的区域内,电势也一定处处相等 | |
| C. | 由B=$\frac{F}{IL}$可知,B与F成正比,与IL成反比 | |
| D. | 电流在磁场中某点不受磁场力作用,则该点的磁感应强度不一定为零 |
 )包括正温度系数电阻器(PTC)和负温度系数电阻器(NTC).正温度系数电阻器(PTC)在温度升高时电阻值增大,负温度系数电阻器(NTC)在温度升高时电阻值减小.热敏电阻的这种特性,常常应用在控制电路中.某实验小组选用下列器材探究通过热敏电阻Rx(常温下阻值约为10Ω)的电流随其两端电压变化的特点.
)包括正温度系数电阻器(PTC)和负温度系数电阻器(NTC).正温度系数电阻器(PTC)在温度升高时电阻值增大,负温度系数电阻器(NTC)在温度升高时电阻值减小.热敏电阻的这种特性,常常应用在控制电路中.某实验小组选用下列器材探究通过热敏电阻Rx(常温下阻值约为10Ω)的电流随其两端电压变化的特点.
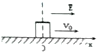 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=4×105N/C,方向与x轴正方向相同.在O处放一个带电量q=-2×10-8 C,质量m=2克的绝缘物块.物块与水平面间的动摩擦系数μ=0.1,沿x轴正方向给物块一个初速度v0=4m/s,如图所示.求:物块最终停止在O左边的位置离O的距离.(g取10m/s2)
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=4×105N/C,方向与x轴正方向相同.在O处放一个带电量q=-2×10-8 C,质量m=2克的绝缘物块.物块与水平面间的动摩擦系数μ=0.1,沿x轴正方向给物块一个初速度v0=4m/s,如图所示.求:物块最终停止在O左边的位置离O的距离.(g取10m/s2)