题目内容
一平行板电容器的电容为C，两极板间的距离为d，上板带正电，电荷量为Q，下板带负电，电荷量也为Q，它们产生的电场在很远处的电势为零．两个带异号电荷的小球用一绝缘刚性杆相连，小球的电荷量均为q，杆长为L，且L＜d．现将它们从很远处移到电容器内两板之间，处于如图所示的静止状态(杆与板面垂直)，在此过程中两个小球克服静电力所做总功的大小等于多少？(设两球移
动过程中极板上电荷分布情况不变)
[ ]
A．
B．
0
C．
D．
答案：A
解析：
解析：
|
讲析：初始两小球在很远处时各自具有的电势能为零，所以Ep0＝0；终点位置两球处于上图所示的静止状态时，设带正电小球的位置为a，该点的电势为 所以静电力对两小球所做的功为W＝Ep0－Ep1＝－ 点评：从功的公式角度出发考虑沿不同方向移动杆与球，无法得出静电力所做功的数值．但从静电力对两个小球做功引起两小球电势能的变化这一角度出发，可以间接求得静电力对两个小球做的总功． |
a，则带正电小球电势能为q
．
，选项A正确．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
一平行板电容器的电容为C，它和三个滑线变阻器按照图示的方式连接成电路．今有一个质量为m的带电油滴静止地悬浮在电容器两板之间．现要油滴下降，可以采用的办法是（ ）
一平行板电容器的电容为C，两板间的距离为d，上板带正电，电量为Q，下板带负电，电量也为Q，它们产生的电场在很远处的电势为零．两个带异号电荷的小球用一绝缘刚性杆相连，小球的电量都为q，杆长为l，且l＜d．现将它们从很远处移到电容器内两板之间，处于图示的静止状态（杆与板面垂直），在此过程中电场力对两个小球所做总功的大小等于多少？（设两球移动过程中极板上电荷分布不变）（ ）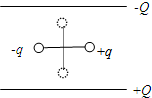
一平行板电容器的电容为C，两板间的距离为d，下板带正电，电荷量为Q．上板带负电，电荷量也为Q，两个带异号电荷的小球用一绝缘刚性杆相连，平行于极板静止放置，小球的电荷量都为q，杆长为l（l＜d）．将杆绕其中点逆时针旋转90°，如图所示，在此过程中电场力对两个小球所做的总功的绝对值为（设两球移动过程中极板上电荷分布情况不变）（ ）