题目内容
如图(甲)所示,为两个有界匀强磁场,磁感应强度大小均为B,方向分别垂直纸面向里和向外,磁场宽度均为L,距磁场区域的左侧L处,有一边长为L的正方形导体线框,总电阻为R,且线框平面与磁场方向垂直,现用外力F使线框以速度v匀速穿过磁场区域,以初始位置为计时起点,规定电流沿逆时针方向时的电动势E为正,磁感线垂直纸面向里时磁通量Φ的方向为正,外力F向右为正。则图(乙)中关于线框中的磁通量Φ、感应电动势E、外力F和电功率P随时间t变化正确的是 ( )

D
解析试题分析:当线框运动L时开始进入磁场,磁通量开始增加,当全部进入时达最大;此后向外的磁通量增加,总磁通减小;当运动到2.5L时,磁通量最小,故A错误;当线圈进入第一个磁场时,由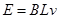 可知,E保持不变,而开始进入第二个磁场时,线框左右两边同时切割磁感线,根据右手定则知,线框左右两边产生的感应电动势方向相同,相当于两个电源相串联,因此电动势是原来的两倍,应为2BLV,故B错误;因安培力总是与运动方向相反,故拉力应一直向右,故C错误;由于线框匀速运动,根据能量转化守恒定律知,电功率等于拉力的功率
可知,E保持不变,而开始进入第二个磁场时,线框左右两边同时切割磁感线,根据右手定则知,线框左右两边产生的感应电动势方向相同,相当于两个电源相串联,因此电动势是原来的两倍,应为2BLV,故B错误;因安培力总是与运动方向相反,故拉力应一直向右,故C错误;由于线框匀速运动,根据能量转化守恒定律知,电功率等于拉力的功率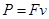 ,因速度不变,而线框在第一个磁场时,电流为定值,拉力也为定值;两边分别在两个磁场中时,由前面的分析可知,电流加倍,故安培力加培,线框左右两边所受安培力方向相同,拉力为原来的4倍,功率为原来的4倍;此后从第二个磁场中离开时,安培力应等于线框在第一个磁场中的安培力,故D正确.所以选D.
,因速度不变,而线框在第一个磁场时,电流为定值,拉力也为定值;两边分别在两个磁场中时,由前面的分析可知,电流加倍,故安培力加培,线框左右两边所受安培力方向相同,拉力为原来的4倍,功率为原来的4倍;此后从第二个磁场中离开时,安培力应等于线框在第一个磁场中的安培力,故D正确.所以选D.
考点:本题考查导体切割磁感线时的感应电动势、安培力、右手定则、法拉第电磁感应定律、电磁感应中的能量转化及闭合电路的欧姆定律.

 中考解读考点精练系列答案
中考解读考点精练系列答案关于电磁感应现象中,通过线圈的磁通量与感应电动势关系正确的是
| A.穿过线圈的磁通量不变,感应电动势不为零且不变 |
| B.穿过线圈的磁通量增大,感应电动势也一定增大 |
| C.穿过线圈的磁通量减小,感应电动势也一定减小 |
| D.穿过线圈的磁通量增大,感应电动势可能不变 |
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1.用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后
| A.金属棒ab、cd都做匀速运动 |
| B.金属棒ab上的电流方向是由b向a |
| C.金属棒cd所受安培力的大小等于2F/3 |
| D.两金属棒间距离保持不变 |
如图所示,通电直导线右边有一个矩形线框,线框平面与直导线共面,若使线框逐渐远离(平动)通电导线,则穿过线框的磁通量将( )
| A.逐渐增大 | B.逐渐减小 | C.保持不变 | D.不能确定 |
如图所示,abcd是一个质量为m,边长为L的正方形金属线框。如从图示位置自由下落,在下落h后进人磁感应强度为B的磁场,恰好做匀速直线运动,该磁场的宽度也为L。在这个磁场的正下方3h+L处还有一个磁感应强度未知,但宽度也为L的磁场,金属线框abcd在穿过这个磁场时也恰好做匀速直线运动,那么下列说法正确的是( )
| A.未知磁场的磁感应强度是B/2 |
B.未知磁场的磁感应强度是 |
| C.线框在穿过这两个磁场的过程中产生的电能为4mgL |
| D.线框在穿过这两个磁场的过程中产生的电能为2mgL |
 、通过金属棒的电荷量q以及a、b两端的电势差U随时间t变化的图象中,正确的是
、通过金属棒的电荷量q以及a、b两端的电势差U随时间t变化的图象中,正确的是





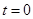 时,将开关S由1掷向2,分别用
时,将开关S由1掷向2,分别用 、
、 、
、 和
和 表示电容器所带的电荷量、棒中的电流、棒的速度大小和加速度大小,则下图所示的图象中正确的是
表示电容器所带的电荷量、棒中的电流、棒的速度大小和加速度大小,则下图所示的图象中正确的是 