题目内容
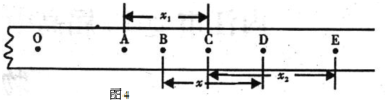
如图所示,是在“探究小车速度随时间变化的规律”的实验中得到的一条纸带.A、B、C、D、E、F、G为测量点,相邻测量点间时间间隔为0.1s,x1=1.20cm,x2=1.60cm,x3=1.98cm,x4=2.38cm,x5=2.79cm,x6=3.18cm.则:

(1)有关操作和测量的说法中不正确的是
A.先释放小车,再接通电源,当小车到达滑轮前及时用手按住它后关闭电源
B.开始释放小车前,应使小车靠近打点计时器
C.测量时应舍去纸带上的密集点,然后选取计数点
D.必须每5个打印点设为一个计数点
(2)将打点计时器打在B、C、D、E、F各测量点时小车的瞬时速度大小填入下表.(数值运算保留三位有效数字)
(3)在平面直角坐标系中作出V-t图象(以测量点B为计时起点).
(4)根据V-t图象能求出小车的加速度吗?若能,请说明求小车加速度的方法并计算小车加速度的大小.

(1)有关操作和测量的说法中不正确的是
AD
AD
A.先释放小车,再接通电源,当小车到达滑轮前及时用手按住它后关闭电源
B.开始释放小车前,应使小车靠近打点计时器
C.测量时应舍去纸带上的密集点,然后选取计数点
D.必须每5个打印点设为一个计数点
(2)将打点计时器打在B、C、D、E、F各测量点时小车的瞬时速度大小填入下表.(数值运算保留三位有效数字)
| 位置 | B | C | D | E | F |
| V(m/s) | 0.140 0.140 |
0.179 0.179 |
0.218 0.218 |
0.259 0.259 |
0.299 0.299 |
(4)根据V-t图象能求出小车的加速度吗?若能,请说明求小车加速度的方法并计算小车加速度的大小.
分析:(1)通过实验的原理以及注意事项确定操作的步骤是否正确.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出各点的瞬时速度.
(3)根据各点的瞬时速度作出v-t图象.
(4)根据图线的斜率求出小车的加速度.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出各点的瞬时速度.
(3)根据各点的瞬时速度作出v-t图象.
(4)根据图线的斜率求出小车的加速度.
解答:解:(1)A、操作时,应先接通电源和释放小车.故A错误.
B、开始释放小车前,小车应靠近打点计时器.故B正确.
C、测量时应舍去纸带上的密集点,然后取计数点.故C正确.
D、若点迹比较密,可以每5个打印点设为一个计数点,若点迹较疏,不需要每5个打印点设为一个计数点.故D错误.
本题选错误的,故选:AD.
(2)某段时间内的平均速度等于中间时刻的瞬时速度,则vB=
=
m/s=0.140m/s.
vC=
=
m/s=0.179m/s.
vD=
=
m/s=0.218m/s.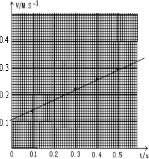
vE=
=
m/s=0.259m/s.
vF=
=
m/s=0.299m/s.
(3)速度时间图线如图所示.
(4)根据v-t图线可以求出加速度,图线的斜率等于小车的加速度,a=
=
=0.4m/s2.
故答案为:(1)AD
(2)0.140,0.179,0.218,0.259,0.299
(3)如图所示
(4)能.求v-t图中的斜率.0.4m/s2
B、开始释放小车前,小车应靠近打点计时器.故B正确.
C、测量时应舍去纸带上的密集点,然后取计数点.故C正确.
D、若点迹比较密,可以每5个打印点设为一个计数点,若点迹较疏,不需要每5个打印点设为一个计数点.故D错误.
本题选错误的,故选:AD.
(2)某段时间内的平均速度等于中间时刻的瞬时速度,则vB=
| x1+x2 |
| 2T |
| 2.80×10-2 |
| 0.2 |
vC=
| x2+x3 |
| 2T |
| (1.60+1.98)×10-2 |
| 0.2 |
vD=
| x3+x4 |
| 2T |
| (1.98+2.38)×10-2 |
| 0.2 |

vE=
| x4+x5 |
| 2T |
| (2.38+2.79)×10-2 |
| 0.2 |
vF=
| x5+x6 |
| 2T |
| (2.79+3.18)×10-2 |
| 0.2 |
(3)速度时间图线如图所示.
(4)根据v-t图线可以求出加速度,图线的斜率等于小车的加速度,a=
| △v |
| △t |
| 0.3-0.1 |
| 0.5 |
故答案为:(1)AD
(2)0.140,0.179,0.218,0.259,0.299
(3)如图所示
(4)能.求v-t图中的斜率.0.4m/s2
点评:解决本题的关键掌握纸带的处理,会通过纸带求解瞬时速度,知道速度时间图线的斜率表示加速度.

练习册系列答案
相关题目
 在探究向心力的大小与质量、角速度和半径之间关系的实验中,如图所示,是研究哪两个物理量之间的关系( )
在探究向心力的大小与质量、角速度和半径之间关系的实验中,如图所示,是研究哪两个物理量之间的关系( ) (2011?宜昌二模)某研究性学习小组在学完《闭合电路欧姆定律》后,利用如图所示的电路来探究电路中各部分的电压、电流随滑动变阻器R阻值变化的关系.电路中R1、R2、R3为三个定值电阻,四个电表均视为理想电表,当滑动变阻器R的滑片P分别置于a、b两个位置时,读出四个电表的两组数据如下:
(2011?宜昌二模)某研究性学习小组在学完《闭合电路欧姆定律》后,利用如图所示的电路来探究电路中各部分的电压、电流随滑动变阻器R阻值变化的关系.电路中R1、R2、R3为三个定值电阻,四个电表均视为理想电表,当滑动变阻器R的滑片P分别置于a、b两个位置时,读出四个电表的两组数据如下: