题目内容
某小组在进行“用单摆测定重力加速度”的实验,已知单摆摆动的摆角小于5°,
(1)单摆的摆长应是球自然下垂时从悬点量至 的距离,此实验在测量周期应从摆球摆到 处开始计时。
(2)某同学先用毫米刻度尺测得悬挂后的摆线长为L,再用游标卡尺测得摆球的直径为d ,如图所示。则该摆球的直径为_____________毫米。

(3)在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t; 该单摆在摆动过程中的周期为 。
(4) 某同学用秒表测得球第40次经过最低点的时间如图所示,则秒表读数为 s;单摆的周期为 s。

(5)用上述物理量的字母符号写出求重力加速度的一般表达式g = .
(6)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中
的 .
A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动时间误记为(n+1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算
(7)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l与T的数据,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率k。则重力加速度g=________。(用k表示)若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则由此图象求得的重力加速度的g (填“偏大”,“偏小”,“无影响”)
(1)球心 最低点(2) 29.8 (3) 2t/n-1 (4) 79.9 4.1 (5)π2(n-1)2(L+d/2)/t2 (6) BD (7) 4π2/k 无影响
【解析】
试题分析:(1)摆长等于摆线长与球半径之和;单摆摆球经过平衡位置的速度最大,最大位移处速度为0,在平衡位置计时误差最小.
(2)摆球的直径为: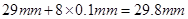
(3)单摆周期为
(4)秒表的读数为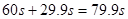 ,单摆周期为
,单摆周期为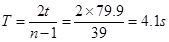
(5)根据周期公式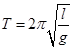 得,
得,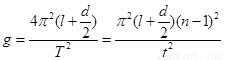
(6)摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,测得的单摆周期变大,根据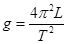 可知,测得的g应偏小.故A错误;实验中误将n次全振动计为n+1次,
可知,测得的g应偏小.故A错误;实验中误将n次全振动计为n+1次,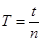 可得周期减小,根据公式
可得周期减小,根据公式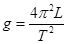 可得g变大,B正确;以摆线长作为摆长来计算,摆长偏小,根据
可得g变大,B正确;以摆线长作为摆长来计算,摆长偏小,根据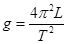 可知,测得的g应偏小.故C错误;D、以摆线长与摆球的直径之和作为摆长来计算,摆长偏大,根据
可知,测得的g应偏小.故C错误;D、以摆线长与摆球的直径之和作为摆长来计算,摆长偏大,根据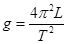 可知,测得的g应偏大.故D正确.故选BD;
可知,测得的g应偏大.故D正确.故选BD;
(7)根据重力加速度的表达式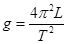 可知,
可知, 图线斜率
图线斜率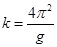 ,则
,则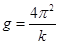 ;若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则实验过程中可能存在的失误是摆长漏加小球半径,从g的表达式可知:g与摆长无关,所以因此失误对由图象求得的重力加速度的g的值无影响.
;若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则实验过程中可能存在的失误是摆长漏加小球半径,从g的表达式可知:g与摆长无关,所以因此失误对由图象求得的重力加速度的g的值无影响.
考点:用单摆测定重力加速度.
点评:常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度,摆长、周期等物理量之间的关系.单摆的周期采用累积法测量可减小误差.对于测量误差可根据实验原理进行分析.

某小组在进行“用单摆测定重力加速度”的实验,已知单摆摆动的摆角小于5°,
(1)单摆的摆长应是球自然下垂时从悬点量至 的距离,此实验在测量周期应从摆球摆到 处开始计时。
(2)某同学先用毫米刻度尺测得悬挂后的摆线长为L,再用游标卡尺测得摆球的直径为d ,如图所示。则该摆球的直径为_____________毫米。
(3)在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t; 该单摆在摆动过程中的周期为 。
(4) 某同学用秒表测得球第40次经过最低点的时间如图所示,则秒表读数为 s;单摆的周期为 s。
(5)用上述物理量的字母符号写出求重力加速度的一般表达式g = .
(6)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中
的 .
| A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了 |
| B.把n次摆动时间误记为(n+1)次摆动的时间 |
| C.以摆线长作为摆长来计算 |
| D.以摆线长与摆球的直径之和作为摆长来计算 |
 某实验中学的学习小组在进行科学探测时,一位同学利用绳索顺利跨越了一道山涧,他先用绳索做了一个单摆(秋千),通过摆动,使自身获得足够大的速度后再平抛到山涧对面,如图所示,若他的质量是M,所用绳长为L,在摆到最低点B处时的速度为v,离地高度为h,当地重力加速度为g.
某实验中学的学习小组在进行科学探测时,一位同学利用绳索顺利跨越了一道山涧,他先用绳索做了一个单摆(秋千),通过摆动,使自身获得足够大的速度后再平抛到山涧对面,如图所示,若他的质量是M,所用绳长为L,在摆到最低点B处时的速度为v,离地高度为h,当地重力加速度为g.
 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d(读数如图).
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d(读数如图).