��Ŀ����
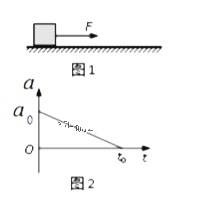
����Ŀ����ͼ��ʾ�������⻬ƽ�н�������֮����ڷ���ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ļ��ΪL�����費�ơ���������ֱ�ڵ�����ã�����Ϊm�������͵���ɺ��Բ��ơ����ڵ�����˽���һ������ΪR�Ķ�ֵ���裬��������ʩ��һ��ˮƽ���ҵĺ���F������ʱ![]() ��������ﵽ����ٶȡ�
��������ﵽ����ٶȡ�

![]() ������������ٶ�
������������ٶ�![]() �Ƕ��٣�
�Ƕ��٣�
![]() ��������Ӿ�ֹ�ﵽ����ٶȵĹ����С�ͨ������R�ĵ����q��
��������Ӿ�ֹ�ﵽ����ٶȵĹ����С�ͨ������R�ĵ����q��
![]() ��ͼ����ʾ���������軻��һ�����ݴ�СΪC�ĵ�����
��ͼ����ʾ���������軻��һ�����ݴ�СΪC�ĵ�����![]() ��Ϊ��������ŵ��˲�����
��Ϊ��������ŵ��˲�����![]() ����������ɾ�ֹ��ʼ����ʱ��t�����������ĵ����Q��
����������ɾ�ֹ��ʼ����ʱ��t�����������ĵ����Q��
���𰸡�![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ٶ����ʱ��������������밲����ƽ�⣬����ƽ����������������ʽ���иʽ��ʽ��������⼴�ɣ���2�����ݷ��ɵĵ�Ÿ�Ӧ������ʽ���ƽ����Ӧ�綯�ơ�����ŷķ������ʽ���ƽ���������ٸ��ݵ������������������3������ţ�ٵڶ����ɺ͵����Ķ���ʽ���õ��������ļ��ٶȱ���ʽ���ٷ������˶�������ɷ����ڵ�Ÿ�Ӧ�������MN�������ĸ�Ӧ�綯�ƣ��õ��������ĵ�ѹ���Ӷ�����������ĵ�����
��1�������������������ʱ�����ٶ�Ϊ�㣬�����ٶȴﵽ���F=BIL=![]()
�ɴ˿ɵý�����������ٶ���vmax=![]()
��2���ɶ������ɿɵã�(F-![]() )t0=mvmax
)t0=mvmax
����![]() =
=![]()
��ý������Ӿ�ֹ�ﵽ����ٶȵĹ������˶��ľ�����x=![]() -
-![]()
ͨ������R�ĵ������q=![]() =
=![]() -
-![]()
��3���赼����˶����ٶ�Ϊa��ijʱװ���������ٶ�Ϊv1������![]() t��������ٶ�Ϊv2��������������ĵ���
t��������ٶ�Ϊv2��������������ĵ���![]() ������
������![]() ΪI����:F-BIL=ma
ΪI����:F-BIL=ma
������I=![]() =
=![]()
����![]() E=BLv2-BLv1=BL
E=BLv2-BLv1=BL![]() v��a=
v��a=![]()
������ʽ�ã�a=![]()
��ˣ�������������ȼ���ֱ���˶����������е�������ԣ�ƽ�а������������ѹU�뵼����и�Ÿ��߲����ĸ�Ӧ�綯��E��ȣ��������ĵ������Q=CBLat=![]()
����1��������������ٶ�![]() ��
��![]() ��
��
��2���������Ӿ�ֹ�ﵽ����ٶȵĹ����У�ͨ������R�ĵ����qΪ![]() ��
��
��3���������ɾ�ֹ��ʼ����ʱ��t�����������ĵ����QΪ![]() ��
��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�