Question

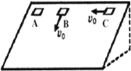
【题目】如图，半径为R的四分之一圆内存在匀强磁场，磁感应强度大小为B，方向垂直纸面向里，半径OA水平。在圆的最低点C有一粒子源，它正以相同速率在纸面内向各个方向发射质量为m、带电量为q（q＞0）的粒子，速率大小为。在圆弧上AC有粒子射出，B为圆弧上一点，∠AOB等于60°，不计粒子所受重力，下列说法正确的是（　　）

A.所有从圆弧上出来的粒子的速度方向都平行

B.所有从圆弧上出来的粒子在磁场中运动时间都相等

C.从A处射出的粒子与从B处射出的粒子在磁场中运动时间之比3∶1

D.从A处射出的粒子与从B处射出的粒子在磁场中的速度偏转角之比为3∶2

Answer 1

【答案】AC

【解析】

A．粒子在磁场中做圆周运动，洛伦兹力提供向心力，由牛顿第二定律得

解得

r=R

粒子在磁场中做圆周运动的轨道半径与磁场半径相等；
粒子沿CO方向入射其运动轨迹如图所示，则OCO2A是正方形，是菱形，粒子偏转角为为90°；粒子沿其它方向入射，由于C点不变，OC不变，四边形的四个边相等，四边形永远是菱形，则O2B一定平行与OC，速度一定沿水平方向射出，故A正确；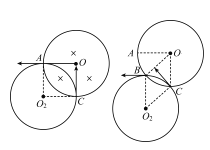
B．沿不同方向射入的粒子在磁场中的偏转角度θ不同，粒子在磁场中的运动时间 不同，故B错误；
CD．由题意可知：∠AOB=60°，则：∠BO2C=30°，两粒子偏转角之比为

90°：30°=3：1

粒子在磁场中的运动时间，粒子在磁场中的运动时间之比等于粒子的偏转角之比，则粒子运动时间之比为3：1，故C正确，D错误；
故选AC。